inamerrata

I have a few things I need to write, but am still a bit too sick with the flu to put together something novel, so instead I’m going to counter-blog Rob Collins recent claim that Money doesn’t matter. Rob’s thoughts are similar to ones I’ve had before, but I think they’re ultimately badly mistaken.

There’s three related, but very different, ways of thinking about money: as a store of value, as a medium of exchange, and as a unit of account. In normal times, dollars (or pounds or euros) work for all three things, so it’s easy to confuse them, but when you’re comparing different moneys some are better at one than another, and when a money starts failing, it will generally fail at each purpose at different rates.

Rob says “Money isn’t wealth” — but that’s wrong. In so far as money serves as a store of value, it is wealth. That’s why having a million dollars in your bank account makes you feel wealthy. The obvious failure mode for store of value is runaway inflation, and that quickly becomes a humanitarian disaster. Money can be one way to store value, but it isn’t the only way: you can store value by investing in artwork, buying property, building a company, or anything else that you expect to be able to sell at some later date. The main difference between those forms of investment versus money is that, ideally, monetary investments have low risk (perhaps the art you bought goes out of fashion and becomes worthless, or the company goes bankrupt, but your million dollars remains a million dollars), and low variance (you won’t make any huge profits, but you won’t make huge losses either). Unlike other assets, money also tends to be very fungible — if you earn $1000, you can spend $100 and have $900 left over; but if you have an artwork worth $1000 it’s a lot harder to sell one tenth of it.

Rob follows up by saying that money is “a thing you can exchange for other things”, which is true — money is a medium of exchange. Ideally it’s cheap and efficient, hard to counterfeit, and easy to verify. This is mostly a matter of technology: pretty gems are good at these things in some ways, coins and paper notes are good in others, cheques kind of work though they’re a bit to easy to counterfeit and a bit too hard to verify, and these days computer networks make credit card systems pretty effective. Ultimately a lot of modern systems have ended up as walled gardens though, and while they’re efficient, they aren’t cheap: whether you consider the 1% fees credit card companies charge, or the 2%-4% fees paypal charges, or the 30% fees from the Apple App Store or Google Play Stores, those are all a lot larger than how much you’d lose accepting a $50 note from someone directly. I have a lot of hope that Bitcoin’s Lightning Network will eventually have a huge impact here. Note that if money isn’t wealth — that is, it doesn’t manage to be a good store of value even in the short term, it’s not a good medium of exchange either: you can’t buy things with it because the people selling will have to immediately get rid of it or they’ll be making a loss; which is why currencies undergoing hyperinflation result in black markets where trade happens in stable currencies.

With modern technology and electronic derivatives, you could (in theory) probably avoid ever holding money. If you’re a potato farmer and someone wants to buy a potato from you, but you want to receive fertilizer for next season’s crop rather than paper money, the exchange could probably be fully automated by an online exchange so that you end up with an extra hundred grams of fertilizer in your next order, with all the details automatically worked out. If you did have such a system, you’d entirely avoid using money as a store of value (though you’d probably be using a credit account with your fertilizer supplier as a store of value), and you’d at least mostly avoid using money as a medium of exchange, but you’d probably still end up using money as a medium of account — that is you’d still be listing the price of potatoes in dollars.

A widely accepted unit of account is pretty important — you need it in order to make contracts work, and it makes comparing different trades much easier. Compare the question “should I sell four apples for three oranges, or two apples for ten strawberries?” with “should I sell four apples for $5, or two apples for $3” and “should I buy three oranges for $5 or ten strawberries for $3?” While I suppose it’s theoretically possible to do finance and economics without a common unit of account, it would be pretty difficult.

This is a pretty key part and it’s where money matters a lot. If you have an employment contract saying you’ll be paid $5000 a month, then it’s pretty important what “$5000” is actually worth. If a few months down the track there’s a severe inflation event, and it’s only worth significantly less, then you’ve just had a severe pay cut (eg, the Argentinian Peso dropped from 5c USD in April to 2.5c USD in September). If you’ve got a well managed currency, that usually means low but positive inflation, so you’ll instead get a 2%-5% pay cut every year — which is considered desirable by economists as it provides an automatic way to devote less resources to less valuable jobs, without managers having to deliberately fire people, or directly cut peoples’ pay. Of course, people tend to be as smart as economists, and many workers expect automatic pay rises in line with inflation anyway.

Rob’s next bit is basically summarising the concept of sticky prices: if there’s suddenly more money to go around, the economy goes weird because people aren’t able to fix prices to match the new reality quickly, causing shortages if there’s more money before there’s higher prices, or gluts (and probably a recession) if there’s less money and people can’t afford to buy all the stuff that’s around — this is what happened in the global financial crisis in 2008/9, though I don’t think there’s really a consensus on whether the blame for less money going around should be put on the government via the Federal Reserve, or the banks, or some other combination of actors.

To summarise so far: money does matter a lot. Having a common unit of account so you can give things meaningful prices is essential, having a convenient store of value that you can use for large and small amounts, and being able to easily trade it for goods and services is a really big deal. Screwing it up hurts people directly, and can be really massively harmful. You could probably use something different for medium of exchange than method of account (eg, a lot of places accepting cryptocurrencies use the cryptocurrency as medium of exchange, but use regular dollars for both store of value and pricing); but without a store of value you don’t have a medium of exchange, and once you’ve got a method of account, having it also work as a store of value is probably too convenient to skip.

But all that said, money is just a tool — generally money isn’t what anyone wants, people want the things they can get with money. Rob phrases that as “resources and productivity”, which is fine; I think the economics jargon would be “real GDP” — ie, the actual stuff that goes into GDP, as opposed to the dollar figure you put on it. Things start going wonky quickly though, in particular with the phrase “If, given the people currently in our country, and what they are being paid to do today, we have enough resources, and enough labour-and-productivity to …” — this starts mixing up nominal and real terms: people expect to be paid in dollars, but resources and labour are real units. If you’re talking about allocating real resources rather than dollars, you need to balance that against paying people in real resources rather than dollars as well, because that’s what they’re going to buy with their nominal dollars.

Why does that matter? Ultimately, because it’s very easy to get the maths wrong and not have your model of the national economy balanced: you allocate some resources here, pay some money there, then forget that the people you paid will use that money to reallocate some resources. If the error’s large enough and systemic enough, you’ll get runaway inflation and all the problems that go with it.

Rob has a specific example here: an unemployed (but skilled) builder, and a homeless family (who need a house built). Why not put the two together, magic up some money to prime the system and build a house? Voila the builder has a job, and the family has a home and everyone is presumably better off. But you can do the same thing without money: give the homeless family a loaded gun and introduce them to the builder: the builder has a job, and the family get a home, and with any luck the bullet doesn’t even get used! The key problem was that we didn’t inspect the magic sufficiently: the builder doesn’t want a job, or even money, he wants the rewards that the job and the money obtain. But where do those rewards come from? Maybe we think the family will contribute to the economy once they have a roof over their heads — if so, we could commit to that: forget the gun, the family goes to a bank, demonstrates they’ll be able to earn an income in future, and takes out a loan, then goes to the builder and pays for their house, and then they get jobs and pay off their mortgage. But if the house doesn’t let the family get jobs and pay for the home, the things the builder buys with his pay have to come from somewhere, and the only way that can happen is by making everyone else in the country a little bit poorer. Do that enough, and everyone who can will move to a different country that doesn’t have that problem.

Loans are a serious answer to the problem in general: if the family is going to be able to work and pay for the house eventually, the problem isn’t one of money, it’s one of risk: whoever currently owns the land, or the building supplies, or whatever doesn’t want to take the risk they’ll never see anything for letting the house get built. But once you have someone with founds who is willing to take the risk, things can start happening without any change in government policies. Loaning directly to the family isn’t the only way; you could build a set of units on spec, and run a charity that finds disadvantaged families, and sets them up, and maybe provide them with training or administrative support to help them get into the workforce, at which point they can pay you back and you can either turn a profit, or help the next disadvantaged family; or maybe both.

Rob then asks himself a bunch of questions, which I’ll answer too:

• What about the foreign account deficit? (It doesn’t matter in the first place, unless perhaps you’re anti-immigrant, and don’t want foreigners buying property)
• What about the fact that lots of land is already owned by someone? (There’s enough land in Australia outside of Sydney/Melbourne that this isn’t an issue; I don’t have any idea what it’s like in NZ, but see Tokyo for ways of housing people on very little land if it is a problem)
• How do we fairly get the family the house they deserve? (They don’t deserve a house; if they want a nice house, they should work and save for it. If they’re going through hard times, and just need a roof over their heads, that’s easily and cheaply done, and doesn’t need a lot of space)
• Won’t some people just ride on the coat-tails of others? (Yes, of course they will. That’s why you target the assistance to help them survive and get back on their feet, and if they want to get whatever it is they think they deserve, they can work for it, like everyone else)
• Isn’t this going to require taking things other people have already earnt? (Generally, no: people almost always buy houses with loans, for instance, rather than being given them for free, or buying them outright; there might be a need to raises taxes, but not to fundamentally change them, though there might be other reasons why larger reform is worthwhile)

This brings us back to the claim Rob makes at the start of his blog: that the whole “government cannot pay for healthcare” thing is nonsense. It’s not nonsense: at the extreme, government can’t pay for enough healthcare for everyone to live to 120 while feeling like they’re 30. Even paying enough for everyone to have the best possible medical care isn’t feasible: even if NZ has a uniform health care system with 100% of its economy devoted to caring for the sick and disabled, there’s going to be a specialist facility somewhere overseas that does a better job. If there isn’t a uniform healthcare system (and there won’t be, even if only due to some doctors/nurses being individually more talented), there’ll also be better and worse places to go in NZ. The reason we have worrying fiscal crises in healthcare and aged support isn’t just a matter of money that can be changed with inflation, it’s that the real economic resources we’re expecting to have don’t align with the promises we’re already making. Those resources are usually expressed in dollar terms, but that’s because having a unit of account makes talking about these things easier: we don’t have to explicitly say “we’ll need x surgeons and y administrators and z MRI machines and w beds” but instead can just collect it all and say “we’ll need x billion dollars”, and leave out a whole mass of complexity, while still being reasonably accurate.

(Similar with “education” — there are limits to how well you can educate everyone, and there’s a trade off between how many resources you might want to put into educating people versus how many resources other people would prefer. In a democracy, that’s just something that’s going to get debated. As far as land goes, on the other hand, I don’t think there’s a fundamental limit to the government taking control over land it controls, though at least in Australia I believe that’s generally considered to be against the vibe of the constitution. If you want to fairly compensate land holders for taking their land, that goes back to budget negotiations and government priorities, and doesn’t seem very interesting in the abstract)

Probably the worst part of Rob’s blog is this though: “We get 10% less things done. Big deal.” Getting 10% less things done is a disaster, for comparison the Great Recession in the US had a GDP drop of less than half that, at -4.2% between 2007Q4 and 2009Q2, and the Great Depression was supposedly about -15% between 1929 and 1932. Also, saying “we’d want 90% of folk not working” is pretty much saying “90% of folk have nothing of value to contribute to anyone else”, because if they did, they could do that, be paid for it, and voila, they’re working. That simply doesn’t seem plausible to me, and I think things would get pretty ugly if it ended up that way despite it’s implausibility.

(Aside: for someone who’s against carbs, “potato farmer” as the go to example seems an interesting choice… )

I figured “Someday we’ll find it: the Bitcoin connection; the coders, exchanges, and me” was too long for a title. Anyhoo, since very late February I’ve been gainfully employed in the cryptocurrency space, as a developer on Bitcoin Core at Xapo (it always sounds pretentious to shorten that to “bitcoin core developer” to me).

I mentioned this to Rusty, whose immediate response (after “Congratulations”) was “Xapo is weird”. I asked if he could name a Bitcoin company that’s not weird — turns out that’s still an open research problem. A lot of Bitcoin is my kind of weird: open source, individualism, maths, intense arguments, economics, political philosophies somewhere between techno-libertarianism and anarcho-capatalism (“ancap”, which shouldn’t be confused with the safety rating), and a general “we’re going to make the world a better place with more freedom and cleverer technology” vibe of the thing. Xapo in particular is also my kind of weird. For one, it’s founded by Argentinians who have experience with the downsides of inflation (currently sitting at 20% pa, down from 40% and up from 10%), even if that pales in comparison to Venezuela, the world’s current socialist basket case suffering from hyperinflation; and Xapo’s CEO makes what I think are pretty good points about Bitcoin improving global well-being by removing a lot of discretion from monetary policy — as opposed to doing blockchains to make finance more financey, or helping criminals and terrorists out, or just generally getting rich quick. Relatedly, Xapo (seems to me to be) much more of a global company than many cryptocurrency places, which often seem very Silicon Valley focussed (or perhaps NYC, or wherever their respective HQ is); it might be a bit self-indulgent, but I really like being surrounded by people with oddly different cultures, and at least my general impression of a lot of Silicon Valley style tech companies these days is more along the lines of “dysfunctional monoculture” than anything positive. Xapo’s tech choices also seem to be fairly good, or at least in line with my preferences (python! using bitcoin core! microservices!). Xapo is also one of pretty few companies that’s got a strong Bitcoin focus, rather than trying to support every crazy new cryptocurrency or subtoken out there: I tend to think Bitcoin’s the only cryptocurrency that really has good technical and economic fundamentals; so I like “Bitcoin maximilism” in principle, though I guess I’m hard pressed to argue it’s optimal at the business level.

For anyone who follow Bitcoin politics, Xapo might seem a strange choice — Xapo not long ago was on the losing side of the S2X conflict, and why team up with a loser instead of the winners? I don’t take that view for a couple of reasons: I didn’t ever really think doubling the blocksize (the 2X part) was a fundamentally bad idea (not least, because segwit (the S part) already does that and more under some circumstances), but rather the problem was the implementation plan of doing it in just a few months, against the advice of all the most knowledgeable developers, and having an absolutely terrible response when problems with the implementation were found. But although that was probably unavoidable considering the mandate to activate S2X within just a few months, I think the majority of the blame is rightly put on the developers doing the shoddy work, and the solution is for companies to work with developers who can say “no” convincingly, or, preferably, can say “yes, and this is how” long enough in advance that solving the problem well is actually possible. So working with any (or at least most) of the S2X companies just seems like being part of the solution to me. And in any event, I want to live in a world where different viewpoints are welcome and disagreement is okay, and finding out that you’re wrong just means you learned something new, not that you get punished and ostracised.

Likewise, you could argue that anyone who wants to really use Bitcoin should own their private keys, rather than use something like Xapo as a wallet or even a vault, and that working on Xapo is kind-of opposed to the “be your own bank” philosophy at the heart of Bitcoin. My belief is that there’s still a use for banks with Bitcoin: safely storing valuables is hard even when they’re protected by maths instead of (or as well as) locks or guns; so it still makes sense for many people to want to outsource the work of maintaining private keys, and unless you’re an IT professional, it’s probably more sensible to do that to a company that looks kind of like a bank (ie, a custodial wallet like Xapo) rather than one that looks like a software vendor (bitcoin core, electrum, etc) or a hardware vendor (ledger or trezor, eg). In that case, the key benefit that Bitcoin offers is protection from government monetary policy, and, hopefully better/cheaper access or storage of your wealth, which isn’t nothing, even if it’s not fully autonomous control over your wealth.

For the moment, there’s plenty of things to work on at Xapo: I’ve been delaying writing this until I could answer the obvious “when segwit?” question (“now!”), but there’s still more bits to do there, and obviously there are lots of neat things to do improving the app, and even more non-development things to do like dealing with other financial institutions, compliance concerns, and what not. Mostly that’s stuff I help with, but not my focus: instead, the things I’m lucky enough to get to work on are the ones that will make a difference in months/years to come, rather than the next few weeks, which gives me an excuse to keep up to date with things like lightning and Schnorr signatures and work on open source bitcoin stuff in general. It’s pretty fantastic. The biggest risk as I see it is I end up doing too much work on getting some awesome new feature or project prototyped for Xapo and end up having to maintain it, downgrading this from dream job to just a motherforking fantastic one. I mean, aside from the bigger risks like cryptocurrency turns out to be a fad, or we all die from nuclear annihilation or whatever.

I don’t really think disclosure posts are particularly necessary — it’s better to assume everyone has undisclosed interests and biases and judge what they say and do on its own merits. But in the event they are a good idea: financially, I’ve got as yet unvested stock options in Xapo which I plan on exercising and hope will be worth something someday, and some Bitcoin which I’m holding onto and hope will still be worth something some day. I expect those to be highly correlated, so anything good for one will be good for the other. Technically, I think Bitcoin is fascinating, and I’ve put a lot of work into understanding it: I’ve looked through the code, I’ve talked with a bunch of the developers, I’ve looked at a bunch of the crypto, and I’ve even done a graduate diploma in economics over the last couple of years to have some confidence in my ability to judge the economics of it (though to be fair, that wasn’t the reason I had for enrolling initially), and I think it all makes pretty good sense. I can’t say the same about other cryptocurrencies, eg Litecoin’s essentially the same software, but the economics of having a “digital silver” to Bitcoin’s “digital gold” doesn’t seem to make a lot of sense to me, and while Ethereum aims at a bunch of interesting problems and gets the attention it deserves as a result, I’m a long way from convinced it’s got the fundamentals right, and a lot of other cryptocurrency things seem to essentially be scams. Oh, perhaps I should also disclose that I don’t have access to private keys for $10 billion dollars worth of Bitcoin; I’m happily on the open source technology side of things, not on the access to money side.

Of course, my opinions on any of that might change, and my financial interests might change to reflect my changed opinions. I don’t expect to update this blog post, and may or may not post about any new opinions I might form. Which is to say that this isn’t financial advice, I’m not a financial advisor, and if I were, I’m certainly not your financial advisor. If you still want financial advice on crypto, I think Wences’s is reasonable: take 1% of what you’re investing, stick it in Bitcoin, and ignore it for a decade. If Bitcoin goes crazy, great, you’ve doubled your money and can brag about getting in before Bitcoin went up two orders of magnitude; if it goes terrible, you’ve lost next to nothing.

One interesting note: the press is generally reporting Bitcoin as doing terribly this year, maintaining a value of around $7000-$9000 USD after hitting highs of up to $19000 USD mid December. That’s not fake news, but it’s a pretty short term view: for comparison, Wences’s advice linked just above from less than 12 months ago (when the price was about $2500 USD) says “I have seen a number of friends buy at “expensive” prices (say, $300+ per bitcoin)” — but that level of “expensive” is still 20 or 30 times cheaper than today. As a result, in spite of the “bad” news, I think every cryptocurrency company that’s been around for more than a few months is feeling pretty positive at the moment, and most of them are hiring, including Xapo. So if you want to work with me on Xapo’s backend team we’re looking for Python devs. But like every Bitcoin company, expect it to be a bit weird.

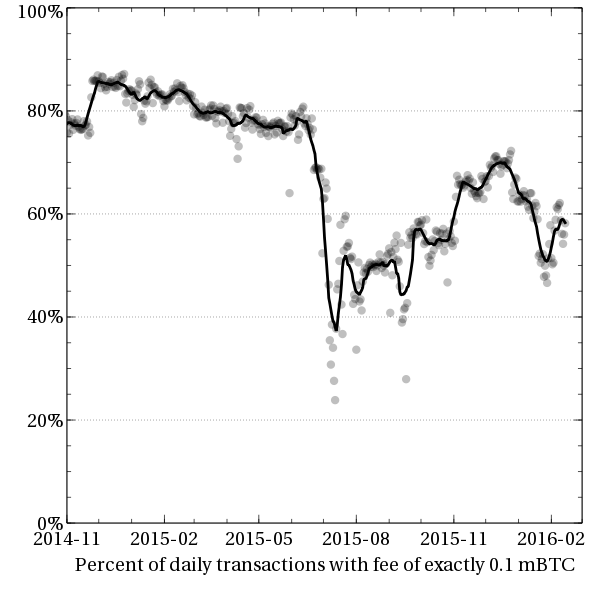
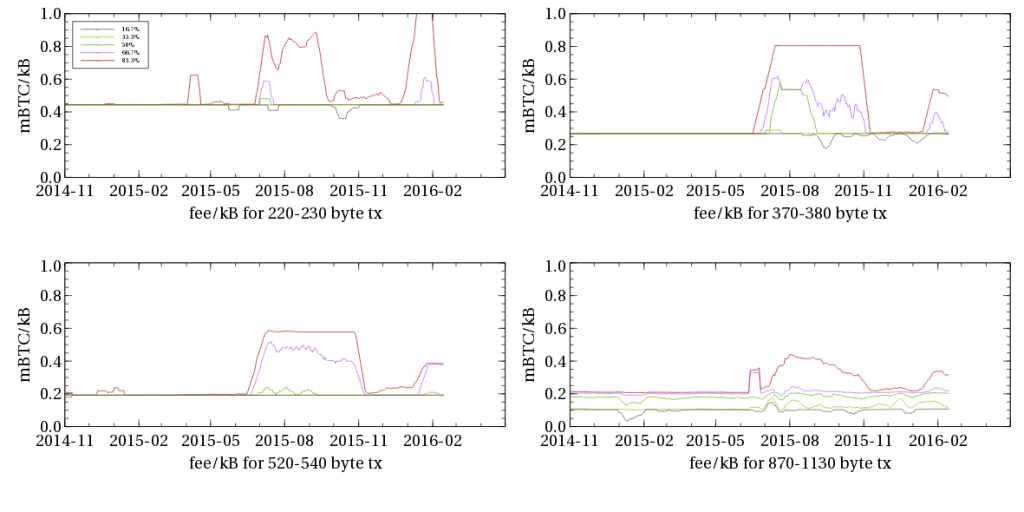
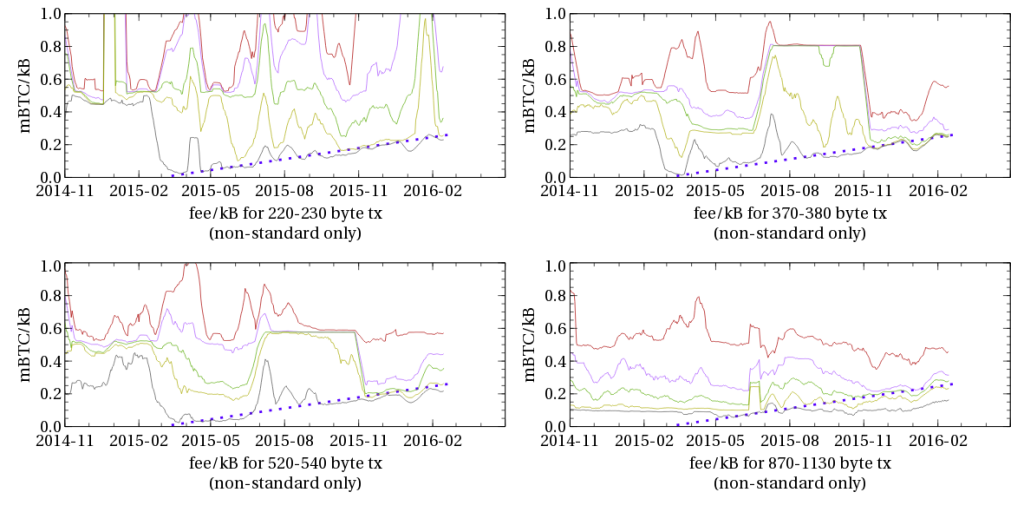
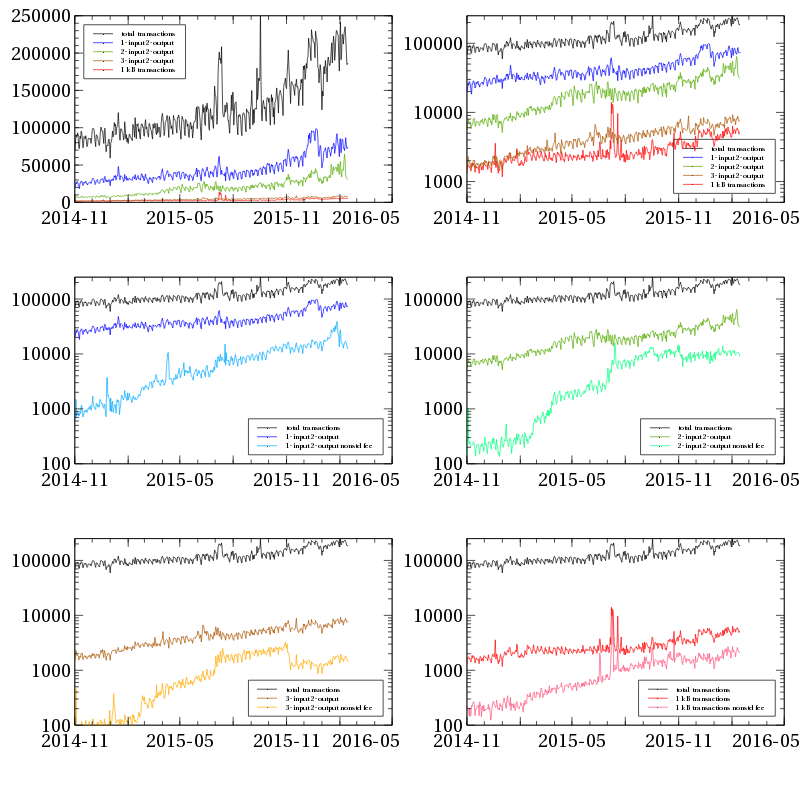
So the first question: is ASICBoost use plausible in the real world?

There are plenty of claims that it’s not:

• “Much conspiracy around #asicboost today. I don’t believe SegWit non-activation has anything to do with AsicBoost!” – Timo Hanke, one of the patent applicants, on twitter
• “Sam Cole, Guy Corem and Timo Hanke, ASIC developers that found AsicBoost independently, agree on this: conflict has nothing to do with it.” – Sergio Demian Lerner, the other patent applicant, also on twitter
• “Bitmain has tested ASICBOOST on the Testnet but has never used ASICBOOST on the mainnet … the ASICBOOST method has not been used by us on the mainnet … Bitmain holds the ASICBOOST patent in China. We can legally use it in our own mining farms in China to profit from it and sell the cloud mining contracts to the public. This, however profitable, is not something we would do for the greater good of Bitcoin.” – Bitmain statement on ASICBoost
• “there’s absolutely nothing but baseless accusations flying around” – Emin Gun Sirer’s take, linked from the Bitmain statement
• “no company would ever produce a chip that would have a switch in to hide that it’s actually an ASICboost chip.” – Sam Cole formerly of KNCMiner which went bankrupt due to being unable to compete with Bitmain in 2016
• “I believe their claim about not activating ASICBoost. It is very small money for them.” – Guy Corem of SpoonDoolies, who independently discovered ASICBoost
• “No one is even using Asicboost.” – Roger Ver (/u/memorydealers) on reddit

A lot of these claims don’t actually match reality though: ASICBoost is implemented in Bitmain miners sold to the public, and since it defaults to off, a switch to hide it is obviously easily possible since it’s disabled by default, contradicting Sam Cole’s take. There’s plenty of circumstantial evidence of ASICBoost-related transaction structuring in blocks, contradicting the basis on which Emin Gun Sirer’s dismisses the claims. The 15%-30% improvement claims that Guy Corem and Sam Cole cite are certainly large enough to be worth looking into — and  Bitmain confirms to have done on testnet. Even Guy Corem’s claim that they only amount to $2,000,000 in savings per year rather than $100,000,000 seems like a reason to expect it to be in use, rather than so little that you wouldn’t bother.

If ASICBoost weren’t in use on mainnet it would probably be relatively straightforward to prove that: Bitmain could publish the benchmarks results they got when testing on testnet, and why that proved not to be worth doing on mainnet, and provide instructions for their customers on how to reproduce their results, for instance. Or Bitmain and others could support efforts to block ASICBoost from being used on mainnet, to ensure no one else uses it, for the greater good of the network — if, as they claim, they’re already not using it, this would come at no cost to them.

To me, much of the rhetoric that’s being passed around seems to be a much better match for what you would expect if ASICBoost were in use, than if it was not. In detail:

• If ASICBoost were in use, and no one had any reason to hide it being used, then people would admit to using it, and would do so by using bits in the block version.
• If ASICBoost were in use, but people had strong reasons to hide that fact, then people would claim not to be using it for a variety of reasons, but those explanations would not stand up to more than casual analysis.
• If ASICBoost were not in use, and it was fairly easy to see there is no benefit to it, then people would be happy to share their reasoning for not using it in detail, and this reasoning would be able to be confirmed independently.
• If ASICBoost were not in use, but the reasons why it is not useful require significant research efforts, then keeping the detailed reasoning private may act as a competitive advantage.

The first scenario can be easily verified, and does not match reality. Likewise the third scenario does not (at least in my opinion) match reality; as noted above, many of the explanations presented are superficial at best, contradict each other, or simply fall apart on even a cursory analysis. Unfortunately that rules out assuming good faith — either people are lying about using ASICBoost, or just dissembling about why they’re not using it. Working out which of those is most likely requires coming to our own conclusion on whether ASICBoost makes sense.

I think Jimmy Song had some good posts on that topic. His first, on Bitmain’s ASICBoost claims finds some plausible examples of ASICBoost testing on testnet, however this was corrected in the comments as having been performed by Timo Hanke, rather than Bitmain. Having a look at other blocks’ version fields on testnet seems to indicate that there hasn’t been much other fiddling of version fields, so presumably whatever testing of ASICBoost was done by Bitmain, fiddling with the version field was not used; but that in turn implies that Bitmain must have been testing covert ASICBoost on testnet, assuming their claim to have tested it on testnet is true in the first place (they could quite reasonably have used a private testnet instead). Two later posts, on profitability and ASICBoost and Bitmain’s profitability in particular, go into more detail, mostly supporting Guy Corem’s analysis mentioned above. Perhaps interestingly, Jimmy Song also made a proposal to the bitcoin-dev shortly after Greg’s original post revealing ASICBoost and prior to these posts; that proposal would have endorsed use of ASICBoost on mainnet, making it cheaper and compatible with segwit, but would also have made use of ASICBoost readily apparent to both other miners and patent holders.

It seems to me there are three different ways to look at the maths here, and because this is an economics question, each of them give a different result:

• Greg’s maths splits miners into two groups each with 50% of hashpower. One group, which is unable to use ASICBoost is assumed to be operating at almost zero profit, so their costs to mine bitcoins are only barely below the revenue they get from selling the bitcoin they mine. Using this assumption, the costs of running mining equipment are calculated by taking the number of bitcoin mined per year (365*24*6*12.5=657k), multiplying that by the price at the time ($1100), and halving the costs because each group only mines half the chain. This gives a cost of mining for the non-ASICBoost group of $361M per year. The other group, which uses ASICBoost, then gains a 30% advantage in costs, so only pays 70%, or $252M, a comparative saving of approximately $100M per annum. This saving is directly proportional to hashrate and ASICBoost advantage, so using Guy Corem’s figures of 13.2% hashrate and 15% advantage, this reduces from $95M to $66M, saving about $29M per annum.
• Guy Corem’s maths estimates Bitmain’s figures directly: looking at the AntPool hashpower share, he estimates 500PH/s in hashpower (or 13.2%); he uses the specs of the AntMiner S9 to determine power usage (0.1 J/GH); he looks at electricity prices in China and estimates $0.03 per kWh; and he estimates the ASICBoost advantage to be 15%. This gives a total cost of 500M GH/s * 0.1 J/GH / 1000 W/kW * $0.03 per kWh * 24 * 365 which is $13.14 M per annum, so a 15% saving is just under $2M per annum. If you assume that the hashpower was 50% and ASICBoost gave a 30% advantage instead, this equates to about 1900 PH/s, and gives a benefit of just under $15M per annum. In order to get the $100M figure to match Greg’s result, you would also need to increase electricity costs by a factor of six, from 3c per kWH to 20c per kWH.
• The approach I prefer is to compare what your hashpower would be keeping costs constant and work out the difference in revenue: for example, if you’re spending $13M per annum in electricity, what is your profit with ASICBoost versus without (assuming that the difficulty retargets appropriately, but no one else changes their mining behaviour). Following this line of thought, if you have 500PH/s with ASICBoost giving you a 30% boost, then without ASICBoost, you have 384 PH/s (500/1.3). If that was 13.2% of hashpower, then the remaining 86.8% of hashpower is 3288 PH/s, so when you stop using ASICBoost and a retarget occurs, total hashpower is now 3672 PH/s (384+3288), and your percentage is now 10.5%. Because mining revenue is simply proportional to hashpower, this amounts to a loss of 2.7% of the total bitcoin reward, or just under $20M per year. If you match Greg’s assumptions (50% hashpower, 30% benefit) that leads to an estimate of $47M per annum; if you match Guy Corem’s assumptions (13.2% hashpower, 15% benefit) it leads to an estimate of just under $11M per annum.

So like I said, that’s three different answers in each of two scenarios: Guy’s low end assumption of 13.2% hashpower and a 15% advantage to ASICBoost gives figures of $29M/$2M/$11M; while Greg’s high end assumptions of 50% hashpower and 30% advantage give figures of $100M/$15M/$47M. The differences in assumptions there is obviously pretty important.

I don’t find the assumptions behind Greg’s maths realistic: in essence, it assumes that mining be so competitive that it is barely profitable even in the short term. However, if that were the case, then nobody would be able to invest in new mining hardware, because they would not recoup their investment. In addition, even if at some point mining were not profitable, increases in the price of bitcoin would change that, and the price of bitcoin has been increasing over recent months. Beyond that, it also assumes electricity prices do not vary between miners — if only the marginal miner is not profitable, it may be that some miners have lower costs and therefore are profitable; and indeed this is likely the case, because electricity prices vary over time due to both seasonal and economic factors. The method Greg uses does is useful for establishing an upper limit, however: the only way ASICBoost could offer more savings than Greg’s estimate would be if every block mined produced less revenue than it cost in electricity, and miners were making a loss on every block. (This doesn’t mean $100M is an upper limit however — that estimate was current in April, but the price of bitcoin has more than doubled since then, so the current upper bound via Greg’s maths would be about $236M per year)

A downside to Guy’s method from the point of view of outside analysis is that it requires more information: you need to know the efficiency of the miners being used and the cost of electricity, and any error in those estimates will be reflected in your final figure. In particular, the cost of electricity needs to be a “whole lifecycle” cost — if it costs 3c/kWh to supply electricity, but you also need to spend an additional 5c/kWh in cooling in order to keep your data-centre operating, then you need to use a figure of 8c/kWh to get useful results. This likely provides a good lower bound estimate however: using ASICBoost will save you energy, and if you forget to account for cooling or some other important factor, then your estimate will be too low; but that will still serve as a loose lower bound. This estimate also changes over time however; while it doesn’t depend on price, it does depend on deployed hashpower — since total hashrate has risen from around 3700 PH/s in April to around 6200 PH/s today, if Bitmain’s hashrate has risen proportionally, it has gone from 500 PH/s to 837 PH/s, and an ASICBoost advantage of 15% means power cost savings have gone from $2M to $3.3M per year; or if Bitmain has instead maintained control of 50% of hashrate at 30% advantage, the savings have gone from $15M to $25M per year.

The key difference between my method and both Greg’s and Guy’s is that they implicitly assume that consuming more electricity is viable, and costs simply increase proportionally; whereas my method assumes that this is not viable, and instead that sufficient mining hardware has been deployed that power consumption is already constrained by some other factor. This might be due to reaching the limit of what the power company can supply, or the rating of the wiring in the data centre, or it might be due to the cooling capacity, or fire risk, or some other factor. For an operation spanning multiple data centres this may be the case for some locations but not others — older data centres may be maxed out, while newer data centres are still being populated and may have excess capacity, for example. If setting up new data centres is not too difficult, it might also be true in the short term, but not true in the longer term — that is having each miner use more power due to disabling ASICBoost might require shutting some miners down initially, but they may be able to be shifted to other sites over the course of a few weeks or month, and restarted there, though this would require taking into account additional hosting costs beyond electricity and cooling. As such, I think this is a fairly reasonable way to produce an plausible estimate, and it’s the one I’ll be using. Note that it depends on the bitcoin price, so the estimates this method produces have also risen since April, going from $11M to $24M per annum (13.2% hash, 15% advantage) or from $47M to $103M (50% hash, 30% advantage).

The way ASICBoost works is by allowing you to save a few steps: normally when trying to generate a proof of work, you have to do essentially six steps:

1. A = Expand( Chunk1 )
2. B = Compress( A, 0 )
3. C = Expand( Chunk2 )
4. D = Compress( C, B )
5. E = Expand( D )
6. F = Compress( E )

The expected process is to do steps (1,2) once, then do steps (3,4,5,6) about four billion (or more) times, until you get a useful answer. You do this process in parallel across many different chips. ASICBoost changes this process by observing that step (3) is independent of steps (1,2) — so by finding a variety of Chunk1s — call them Chunk1-A, Chunk1-B, Chunk1-C and Chunk1-D that are each compatible with a common Chunk2. In that case, you do steps (1,2) four times for each different Chunk1, then do step (3) four billion (or more) times, and do steps (4,5,6) 16 billion (or more) times, to get four times the work, while saving 12 billion (or more) iterations of step (3). Depending on the number of Chunk1’s you set yourself up to find, and the relative weight of the Expand versus Compress steps, this comes to (n-1)/n / 2 / (1+c/e), where n is the number of different Chunk1’s you have. If you take the weight of Expand and Compress steps as about equal, it simplifies to 25%*(n-1)/n, and with n=4, this is 18.75%. As such, an ASICBoost advantage of about 20% seems reasonably practical to me. At 50% hash and 20% advantage, my estimates for ASICBoost’s value are $33M in April, and $72M today.

So as to the question of whether you’d use ASICBoost, I think the answer is a clear yes: the lower end estimate has risen from $2M to $3.3M per year, and since Bitmain have acknowledged that AntMiner’s support ASICBoost in hardware already, the only additional cost is finding collisions which may not be completely trivial, but is not difficult and is easily automated.

If the benefit is only in this range, however, this does not provide a plausible explanation for opposing segwit: having the Bitcoin industry come to a consensus about how to move forward would likely increase the bitcoin price substantially, definitely increasing Bitmain’s mining revenue — even a 2% increase in price would cover their additional costs. However, as above, I believe this is only a lower bound, and a more reasonable estimate is on the order of $11M-$47M as of April or $24M-$103M as of today. This is a much more serious range, and would require an 11%-25% increase in price to not be an outright loss; and a far more attractive proposition would be to find a compromise position that both allows the industry to move forward (increasing the price) and allows ASICBoost to remain operational (maintaining the cost savings / revenue boost).

It’s possible to take a different approach to analysing the cost-effectiveness of mining given how much you need to pay in electricity costs. If you have access to a lot of power at a flat rate, can deal with other hosting issues, can expand (or reduce) your mining infrastructure substantially, and have some degree of influence in how much hashpower other miners can deploy, then you can derive a formula for what proportion of hashpower is most profitable for you to control.

In particular, if your costs are determined by an electricity (and cooling, etc) price, E, in dollars per kWh and performance, r, in Joules per gigahash, then given your hashrate, h in terahash/second, your power usage in watts is (h*1e3*r), and you run this for 600 seconds on average between each block (h*r*6e5 Ws), which you divide by 3.6M to convert to kWh (h*r/6), then multiply by your electricity cost to get a dollar figure (h*r*E/6). Your revenue depends on the hashrate of the everyone else, which we’ll call g, and on average you receive (p*R*h/(h+g)) every 600 seconds where p is the price of Bitcoin in dollars and R is the reward (subsidy and fees) you receive from a block. Your profit is just the difference, namely h*(p*R/(h+g) – r*E/6). Assuming you’re able to manufacture and deploy hashrate relatively easily, at least in comparison to everyone else, you can optimise your profit by varying h while the other variables (bitcoin price p, block reward R, miner performance r, electricity cost E, and external hashpower g) remain constant (ie, set the derivative of that formula with respect to h to zero and simplify) which gives a result of 6gpR/Er = (g+h)^2.

This is solvable for h (square root both sides and subtract g), but if we assume Bitmain is clever and well funded enough to have already essentially optimised their profits, we can get a better sense of what this means. Since g+h is just the total bitcoin hashrate, if we call that t, and divide both sides, we get 6gpR/Ert = t, or g/t = (Ert)/(6pR), which tells us what proportion of hashrate the rest of the network can have (g/t) if Bitmain has optimised its profits, or, alternative we can work out h/t = 1-g/t = 1-(Ert)/(6pR) which tells us what proportion of hashrate Bitmain will have if it has optimised its profits.  Plugging in E=$0.03 per kWH, r=0.1 J/GH, t=6e6 TH/s, p=$2400/BTC, R=12.5 BTC gives a figure of 0.9 – so given the current state of the network, and Guy Corem’s cost estimate, Bitmain would optimise its day to day profits by controlling 90% of mining hashrate. I’m not convinced $0.03 is an entirely reasonable figure, though — my inclination is to suspect something like $0.08 per kWh is more reasonable; but even so, that only reduces Bitmain’s optimal control to around 73%.

Because of that incentive structure, if Bitmain’s current hashrate is lower than that amount, then lowering manufacturing costs for own-use miners by 15% (per Sam Cole’s estimates) and lowering ongoing costs by 15%-30% by using ASICBoost could have a compounding effect by making it easier to quickly expand. (It’s not clear to me that manufacturing a line of ASICBoost-only miners to reduce manufacturing costs by 15% necessarily makes sense. For one thing, this would come at a cost of not being able to mine with them while they are state of the art, then sell them on to customers once a more efficient model has been developed, which seems like it might be a good way to manage inventory. For another, it vastly increases the impact of ASICBoost not being available: rather than simply increasing electricity costs by 15%-30%, it would mean reducing output to 10%-25% of what it was, likely rendering the hardware immediately obsolete)

Using the same formula, it’s possible to work out a ratio of bitcoin price (p) to hashrate (t) that makes it suboptimal for a manufacturer to control a hashrate majority (at least just due to normal mining income): h/t < 0.5, 1-Ert/6pR < 0.5, so t > 3pR/Er. Plugging in p=2400, R=12.5, e=0.08, r=0.1, this gives a total hash rate of 11.25M TH/s, almost double the current hash rate. This hashrate target would obviously increase as the bitcoin price increases, halve if the block reward halves (if a fall in the inflation subsidy is not compensated by a corresponding increase in fee income eg), increase if the efficiency of mining hardware increases, and decrease if the cost of electricity increases. For a simpler formula, assuming the best hosting price is $0.08 per kWh, and while the Antminer S9’s efficiency at 0.1 J/GH is state of the art, and the block reward is 12.5 BTC, the global hashrate in TH/s should be at least around 5000 times the price (ie 3R/Er = 4787.5, near enough to 5000).

Note that this target also sets a limit on the range at which mining can be profitable: if it’s just barely better to allow other people to control >50% of miners when your cost of electricity is E, then for someone else whose cost of electricity is 2*E or more, optimal profit is when other people control 100% of hashrate, that is, you don’t mine at all. Thus if the best large scale hosting globally costs $0.08/kWh, then either mining is not profitable anywhere that hosting costs $0.16/kWh or more, or there’s strong centralisation pressure for a mining hardware manufacturer with access to the cheapest electrictiy to control more than 50% of hashrate. Likewise, if Bitmain really can do hosting at $0.03/kWh, then either they’re incentivised to try to control over 50% of hashpower, or mining is unprofitable at $0.06/kWh and above.

If Bitmain (or any mining ASIC manufacturer) is supplying the majority of new hashrate, they actually have a fairly straightforward way of achieving that goal: if they dedicate 50-70% of each batch of ASICs built for their own use, and sell the rest, with the retail price of the sold miners sufficient to cover the manufacturing cost of the entire batch, then cashflow will mostly take care of itself. At $1200 retail price and $500 manufacturing costs (per Jimmy Song’s numbers), that strategy would imply targeting control of up to about 58% of total hashpower. The above formula would imply that’s the profit-maximising target at the current total hashrate and price if your average hosting cost is about $0.13 per kWh. (Those figures obviously rely heavily on the accuracy of the estimated manufacturing costs of mining hardware; at $400 per unit and $1200 retail, that would be 67% of hashpower, and about $0.09 per kWh)

Strategies like the above are also why this analysis doesn’t apply to miners who buy their hardware rather from a vendor, rather than building their own: because every time they increase their own hash rate (h), the external hashrate (g) also increases as a direct result, it is not valid to assume that g is constant when optimising h, so the partial derivative and optimisation is in turn invalid, and the final result is not applicable.

Bitmain’s mining pool, AntPool, obviously doesn’t directly account for 58% or more of total hashpower; though currently they’re the pool with the most hashpower at about 20%. As I understand it, Bitmain is also known to control at least BTC.com and ConnectBTC which add another 7.6%. The other “Emergent Consensus” supporting pools (Bitcoin.com, BTC.top, ViaBTC) account for about 22% of hashpower, however, which brings the total to just under 50%, roughly the right ballpark — and an additional 8% or 9% could easily be pointed at other public pools like slush or f2pool. Whether the “emergent consensus” pools are aligned due to common ownership and contractual obligations or simply similar interests is debatable, though. ViaBTC is funded by Bitmain, and Canoe was built and sold by Bitmain, which means strong contractual ties might exist, however  Jihan Wu, Bitmain’s co-founder, has disclaimed equity ties to BTC.top. Bitcoin.com is owned by Roger Ver, but I haven’t come across anything implying a business relationship between Bitmain and Bitcoin.com beyond supplier and customer. However John McAffee’s apparently forthcoming MGT mining pool is both partnered with Bitmain and advised by Roger Ver, so the existence of tighter ties may be plausible.

It seems likely to me that Bitmain is actually behaving more altruistically than is economically rational according to the analysis above: while it seems likely to me that Bitcoin.com, BTC.top, ViaBTC and Canoe have strong ties to Bitmain and that Bitmain likely has a high level of influence — whether due to contracts, business relationships or simply due to the loyalty and friendship — this nevertheless implies less control over the hashpower than direct ownership and management, and likely less profit. This could be due to a number of factors: perhaps Bitmain really is already sufficiently profitable from mining that they’re focusing on building their business in other ways; perhaps they feel the risks of centralised mining power are too high (and would ultimately be a risk to their long term profits) and are doing their best to ensure that mining power is decentralised while still trying to maximise their return to their investors; perhaps the rate of expansion implied by this analysis requires more investment than they can cover from their cashflow, and additional hashpower is funded by new investors who are simply assigned ownership of a new mining pool, which may helps Bitmain’s investors assure themselves they aren’t being duped by a pyramid scheme and gives more of an appearance of decentralisation.

It seems to me therefore there could be a variety of ways in which Bitmain may have influence over a majority of hashpower:

• Direct ownership and control, that is being obscured in order to avoid an economic backlash that might result from people realising over 50% of hashpower is controlled by one group
• Contractual control despite independent ownership, such that customers of Bitmain are committed to follow Bitmain’s lead when signalling blocks in order to maintain access to their existing hardware, or to be able to purchase additional hardware (an account on reddit appearing to belong to the GBMiners pool has suggested this is the case)
• Contractual control due to offering essential ongoing services, eg support for physical hosting, or some form of mining pool services — maintaining the infrastructure for covert ASICBoost may be technically complex enough that Bitmain’s customers cannot maintain it themselves, but that Bitmain could relatively easily supply as an ongoing service to their top customers.
• Contractual influence via leasing arrangements rather than sale of hardware — if hardware is leased to customers, or financing is provided, Bitmain could retain some control of the hardware until the leasing or financing term is complete, despite not having ownership
• Coordinated investment resulting in cartel-like behaviour — even if there is no contractual relationship where Bitmain controls some of its customers in some manner, it may be that forming a cartel of a few top miners allows those miners to increase profits; in that case rather than a single firm having control of over 50% of hashrate, a single cartel does. While this is technically different, it does not seem likely to be an improvement in practice. If such a cartel exists, its members will not have any reason to compete against each other until it has maximised its profits, with control of more than 70% of the hashrate.

So, conclusions:

• ASICBoost is worth using if you are able to. Bitmain is able to.
• Nothing I’ve seen suggest Bitmain is economically clueless; so since ASICBoost is worth doing, and Bitmain is able to use it on mainnet, Bitmain are using it on mainnet.
• Independently of ASICBoost, Bitmain’s most profitable course of action seems to be to control somewhere in the range of 50%-80% of the global hashrate at current prices and overall level of mining.
• The distribution of hashrate between mining pools aligned with Bitmain in various ways makes it plausible, though not certain, that this may already be the case in some form.
• If all this hashrate is benefiting from ASICBoost, then my estimate is that the value of ASICBoost is currently about $72M per annum
• Avoiding dominant mining manufacturers tending towards supermajority control of hashrate requires either a high global hashrate or a relatively low price — the hashrate in TH/s should be about 5000 times the price in dollars.
• The current price is about $2400 USD/BTC, so the corresponding hashrate to prevent centralisation at that price point is 12M TH/s. Conversely, the current hashrate is about 6M TH/s, so the maximum price that doesn’t cause untenable centralisation pressure is $1200 USD/BTC.

I’ve been trying to make heads or tails of what the heck is going on in Bitcoin for a while now. I’m not sure I’ve actually made that much progress, but I’ve at least got some thoughts that seem coherent now.

First, this post is background for people playing along at home who aren’t familiar with the issues or jargon: Bitcoin is a currency based on an electronic ledger that essentially tracks how much Bitcoin exists, and how someone can be authorised to transfer it to someone else; that ledger is currently about 100GB in size, growing at a rate of about a gigabyte a week. The ledger is updated by miners, who compete by doing otherwise pointless work running cryptographic hashes (and in so doing obtain a “proof of work”), and in return receive a reward (denominated in bitcoin) made up from fees by people transacting and an inflation subsidy. Different miners are competing in an essentially zero-sum game, because fees and inflation are essentially a fixed amount that is (roughly) divided up amongst miners according to how much work they do — so while you get more reward for doing more work, it comes at a cost of other miners receiving less reward.

Because the ledger only grows by (about) a gigabyte each week (or a megabyte per block, which is roughly every ten minutes), there is a limit on how many transactions can be included each week (ie, supply is limited), which both increases fees and limits adoption — so for quite a while now, people in the bitcoin ecosystem with a focus on growth have wanted to work out ways to increase the transaction rate. Initial proposals in mid 2015 suggested allowing miners to regularly determine the limit with no official upper bound (nominally “BIP100“, though never actually formally submitted as a proposal), or to increase by a factor of eight within six months, then double every two years after that, until reaching almost 200 times the current size by 2036 (BIP101), or to increase at a rate of about 17% per annum (suggested on the mailing list, but never formally proposed BIP103). These proposals had two major risks: locking in a lot of growth that may turn out to be unnecessary or actively harmful, and requiring what is called a “hard fork”, which would render the existing bitcoin software unable to track the ledger after the change took affect with the possible outcome that two ledgers would coexist and would in turn cause a range of problems. To reduce the former risk, a minimal compromise proposal was made to “kick the can down the road” and just double the ledger growth rate, then figure out a more permanent solution down the road (BIP102) (or to double it three times — to 2MB, 4MB then 8MB — over four years, per Adam Back). A few months later, some of the devs figured out a way to more or less achieve this that also doesn’t require a hard fork, and comes with a host of other benefits, and proposed an update called “segregated witness” at the December 2015 Scaling Bitcoin conference.

And shortly after that things went completely off the rails, and have stayed that way since. Ultimately there seem to be two camps: one group is happy to deploy segregated witness, and is eager to make further improvements to Bitcoin based on that (this is my take on events); while the other group does not, perhaps due to some combination of being opposed to the segregated witness changes directly, wanting a more direct upgrade immediately, being afraid deploying segregated witness will block other changes, or wanting to take control of the bitcoin codebase/roadmap from the current developers (take this with a grain of salt: these aren’t opinions I share or even find particularly reasonable, so I can’t do them justice when describing them; cf ViaBTC’s post to get that side of the argument made directly, eg)

Most recently, and presumably on the basis that the opposed group are mostly worried that deploying segregated witness will prevent or significantly delay a more direct increase in capacity, a bitcoin venture capitalist, Barry Silbert, organised an agreement amongst a number of companies including many miners, to both activate segregated witness within the next month, and to do a hard fork capacity increase by the end of the year. This is the “segwit2x” project; named because it takes segregated witness, (“segwit”) and then additionally doubles its capacity increase (“2x”). This agreement is not supported by any of the existing dev team, and is being developed by Jeff Garzik (who was behind BIP100 and BIP102 mentioned above) in a forked codebase renamed “btc1“, so if successful, this may also satisfy members of the opposed group motivated by a desire to take control of the bitcoin codebase and roadmap, despite that not being an explicit part of the agreement itself.

To me, the arguments presented for opposing segwit don’t really seem plausible. As far as future development goes, a roadmap was put out in December 2015 and endorsed by many developers that explicitly included a hard fork for increased capacity (“moderate block size increase proposals (such as 2/4/8 …)”), among many other things, so the risk of no further progress happening seems contrary to the facts to me. The core bitcoin devs are extremely capable in my estimation, so replacing them seems a bad idea from the start, but even more than that, they take a notably hands off approach to dictating where Bitcoin will go in future — so, to my mind, it seems like a more sensible thing to try would be working with them to advance the bitcoin ecosystem in whatever direction you want, rather than to try to replace them outright. In that context, it seems particularly notable to me that in the eighteen months between the segregated witness proposal and the segwit2x agreement, there hasn’t been any serious attempt to propose a hard fork capacity increase that meets the core dev’s quality standards; for instance there has never been any code for BIP100, and of the various hard forking codebases that have arisen by advocates of the hard fork approach — Bitcoin XT, Bitcoin Classic, Bitcoin Unlimited, btc1, and Bitcoin ABC — none have been developed in a way that’s suitable for the changes to be reviewed and merged into core via a pull request in the normal fashion. Further, since one of the main criticisms of a hard fork is that deployment costs are higher when it is done in a short time frame (weeks or a few months versus a year or longer), that lack of engagement over the past 18 months followed by a desperate rush now seems particularly poor to me.

A different explanation for the opposition to segwit became public in April, however. ASICBoost is a patent-pending optimisation to the way Bitcoin miners do the work that entitles them to extend the ledger (for which they receive the rewards described earlier), and while there are a few ways of making use of ASICBoost, perhaps the most effective way turns out to be incompatible with segwit. There are three main alternatives to the covert, segwit-incompatible approach, all of which have serious downsides. The first, overt ASICBoost via modifying the block version reveals that you’re using ASICBoost, which would either (a) encourage other miners to also use the optimisation reducing your profits, (b) give the patent holder cause to charge you royalties or cause other problems (assuming the patent is eventually granted and deemed valid), or (c) encourage the bitcoin community at large to change the ecosystem rules so that the optimisation no longer works. The second, mining empty blocks via ASICBoost means you don’t gain any fee income, reducing your revenue and hence profit. And the third, rolling the extranonce to find a collision rather than combining partial transaction trees increases the preparation work by a factor of ten or so, which is probably enough to outweigh the savings from the optimisation in the first place.

If ASICBoost were being used by a significant number of miners, and segregated witness prevents its continued use in practice, then we suddenly have a very plausible explanation for much of the apparent madness: the loss of the optimisation could significantly increase some miners’ costs or reduce their revenue, reducing profit either way (a high end estimate of $100,000,000 per year was given in the original explanation), which would justify significant investment in blocking that change. Further, an honest explanation of the problem would not be feasible, because this would be just as bad as doing the optimisation overtly — it would increase competition, alert the potential patent owners, and might cause the optimisation to be deliberately disabled — all of which would also negatively affect profits. As a result, there would be substantial opposition to segwit, but the reasons presented in public for this opposition would be false, and it would not be surprising if the people presenting these reasons only give half-hearted effort into providing evidence — their purpose is simply to prevent or at least delay segwit, rather than to actually inform or build a new consensus. To this line of thinking the emphasis on lack of communication from core devs or the desire for a hard fork block size increase aren’t the actual goal, so the lack of effort being put into resolving them over the past 18 months from the people complaining about them is no longer surprising.

With that background, I think there are two important questions remaining:

1. Is it plausible that preventing ASICBoost would actually cost people millions in profit, or is that just an intriguing hypothetical that doesn’t turn out to have much to do with reality?
2. If preserving ASICBoost is a plausible motivation, what will happen with segwit2x, given that by enabling segregated witness, it does nothing to preserve ASICBoost?

Well, stay tuned…

Continuing from my previous post on historical Bitcoin fees… Obviously history is fun and all, but it’s safe to say that working out what’s going on now is usually far more interesting and useful. But what’s going on now is… complicated.

First, as was established in the previous post, most transactions are still paying 0.1 mBTC in fees (or 0.1 mBTC per kilobyte, rounded up to the next kilobyte).

Again, as established in the previous post, that’s a fairly naive approach: miners will fill blocks with the smallest transactions that pay the highest fees, so if you pay 0.1 mBTC for a small transaction, that will go in quickly, but if you pay 0.1 mBTC for a large transaction, it might not be included in the blockchain at all.

It’s essentially like going to a petrol station and trying to pay a flat $30 to fill up, rather than per litre (or per gallon); if you’re riding a scooter, you’re probably over paying; if you’re driving an SUV, nobody will want anything to do with you. Pay per litre, however, and you’ll happily get your tank filled, no matter what gets you around.

But back in the bitcoin world, while miners have been using the per-byte approach since around July 2012, as far as I can tell, users haven’t really even had the option of calculating fees in the same way prior to early 2015, with the release of Bitcoin Core 0.10.0. Further, that release didn’t just change the default fees to be per-byte rather than (essentially) per-transaction; it also dynamically adjusted the per-byte rate based on market conditions — providing an estimate of what fee is likely to be necessary to get a confirmation within a few blocks (under an hour), or within ten or twenty blocks (two to four hours).

There are a few sites around that make these estimates available without having to run Bitcoin Core yourself, such as bitcoinfees.21.co, or bitcoinfees.guthub.io. The latter has a nice graph of recent fee rates:

You can see from this graph that the estimated fee rates vary over time, both in the peak fee to get a transaction confirmed as quickly as possible, and in how much cheaper it might be if you’re willing to wait.

Of course, that just indicates what you “should” be paying, not what people actually are paying. But since the blockchain is a public ledger, it’s at least possible to sift through the historical record. Rusty already did this, of course, but I think there’s a bit more to discover. There’s three ways in which I’m doing things differently to Rusty’s approach: (a) I’m using quantiles instead of an average, (b) I’m separating out transactions that pay a flat 0.1 mBTC, (c) I’m analysing a few different transaction sizes separately.

To go into that in a little more detail:

• Looking at just the average values doesn’t seem really enlightening to me, because it can be massively distorted by a few large values. Instead, I think looking at the median value, or even better a few percentiles is likely to work better. In particular I’ve chosen to work with “sextiles”, ie the five midpoints you get when splitting each day’s transactions into sixths, which gives me the median (50%), the tertiles (33% and 66%), and two additional points showing me slightly more extreme values (16.7% and 83.3%).
• Transactions whose fees don’t reflect market conditions at all, aren’t really interesting to analyse — if there are enough 0.1 mBTC, 200-byte transactions to fill a block, then a revenue maximising miner won’t mine any 400-byte transactions that only pay 0.1 mBTC, because they could fit two 200-byte transactions in the same space and get 0.2 mBTC; and similarly for transactions of any size larger than 200-bytes. There’s really nothing more to it than that. Further, because there are a lot of transactions that are essentially paying a flat 0.1 mBTC fee, they make it fairly hard to see what the remaining transactions are doing — but at least it’s easy to separate them out.
• Because the 0.10 release essentially made two changes at once (namely, switching from a hardcoded default fee to a fee that varies on market conditions, and calculating the fee based on a per-byte rate rather than essentially a per-transaction rate) it can be hard to see which of these effects are taking place. By examining the effect on transactions of a particular size, we can distinguish the effects however: using a per-transaction fee will result in different transactions sizes paying different per-byte rates, while using per-byte fee will result in the transactions of different sizes harmonising at a particular rate. Similarly, using fee estimation will result in the fees for a particular transaction size varying over time; whereas the average fee rate might vary over time simply due to using per-transaction fees while the average size of transactions varies. I’ve chosen four sizes: 220-230 bytes which is the size of a transaction spending a single, standard, pay-to-public-key-hash (P2PKH) input (with a compressed public key) to two P2PKH outputs; 370-380 bytes which matches a transaction spending two P2PKH inputs to two P2PKH outputs; 520-520 bytes which matches a transaction spending three P2PKH inputs to two P2PKH inputs, and 870-1130 bytes which catches transactions around 1kB.

The following set of graphs take this approach, with each transaction size presented as a separate graph. Each graph breaks the relevant transactions into sixths, selecting the sextiles separating each sixth — each sextile is then smoothed over a 2 week period to make it a bit easier to see.

We can make a few observations from this (click the graph to see it at full size):

• We can see that prior to June 2015, fees were fairly reliably set at 0.1 mBTC per kilobyte or part thereof — so 220B transactions paid 0.45 mBTC/kB, 370B transactions paid 0.27 mBTC/kB, 520B transactions paid 0.19 mBTC/kB, and transactions slightly under 1kB paid 0.1 mBTC/kB while transactions slightly over 1kB paid 0.2 mBTC/kB (the 50% median line in between 0.1 mBTC/kB and 0.2 mBTC/kB is likely an artifact of the smoothing). These fees didn’t take transaction size into account, and did not vary depending on market conditions — so they did not reflect changes in demand, how full blocks were, the price of Bitcoin in USD, the hashpower used to secure the blockchain, or any similar factors that might be relevant.
• We can very clearly see that there was a dramatic response to market conditions in late June 2015 — and not coincidentally this was when the “stress tests” or “flood attack” occurred.
• It’s also pretty apparent the market response here wasn’t actually very rational or consistent — eg 220B transactions spiked to paying over 0.8 mBTC/kB, while 1000B transactions only spiked to a little over 0.4 mBTC/kB — barely as much as 220B transactions were paying prior to the stress attack. Furthermore, even while some transactions were paying significantly higher fees, transactions paying standard fees were still going through largely unhindered, making it questionable whether paying higher fees actually achieved anything.
• However, looking more closely at the transactions with a size of around 1000 bytes, we can also see there was a brief period in early July (possibly a very brief period that’s been smeared out due to averaging) where all of the sextiles were above the 0.1 mBTC/kB line — indicating that there were some standard fee paying transactions that were being hindered. That is to say that it’s very likely that during that period, any wallet that (a) wasn’t programmed to calculate fees dynamically, and (b) was used to build a transaction about 1kB in size, would have produced a transaction that would not actually get included in the blockchain. While it doesn’t meet the definition laid out by Jeff Garzik, I think it’s fair to call this a “fee event”, in that it’s an event, precipitated by fee rates, that likely caused detectable failure of bitcoin software to work as intended.
• On the other hand, it is interesting to notice that a similar event has not yet reoccurred since; even during later stress attacks, or Black Friday or Christmas shopping rushes.

As foreshadowed, we can redo those graphs with transactions paying one of the standard fees (ie exactly 0.1 mBTC, 0.01 mBTC, 0.2 mBTC, 0.5 mBTC, 1m BTC, or 10 mBTC) removed:

As before, we can make a few observations from these graphs:

• First, they’re very messy! That is, even amongst the transactions that pay variable fees, there’s no obvious consensus on what the right fee to pay is, and some users are paying substantially more than others.
• In early February, which matches the release of Bitcoin Core 0.10.0, there was a dramatic decline in the lowest fees paid — which is what you would predict if a moderate number of users started calculating fees rather than using the defaults, and found that paying very low fees still resulted in reasonable confirmation times. That is to say, wallets that dynamically calculate fees have substantially cheaper transactions.
• However, those fees did not stay low, but have instead risen over time — roughly linearly. The blue dotted trend line is provided as a rough guide; it rises from 0 mBTC/kB on 1st March 2015, to 0.27 mBTC/kB on 1st March 2016. That is, market driven fees have roughly risen to the same cost per-byte as a 2-input, 2-output transaction, paying a flat 0.1 mBTC.

At this point, it’s probably a good idea to check that we’re not looking at just a handful of transactions when we remove those paying standard 0.1 mBTC fees. Graphing the number of transactions per day of each type (ie, total transactions, 220 byte transactions (1-input, 2-output), 370 byte transactions (2-input, 2-output), 520 byte transactions (3-input, 2-output), and 1kB transactions shows that they all increased over the course of the year, and that there are far more small transactions than large ones. Note that the top-left graph has a linear y-axis; while the other graphs use a logarithmic y-axis — so that each step in the vertical indicates a ten-times increase in number of transactions per day. No smoothing/averaging has been applied.

We can see from this that by and large the number of transactions of each type have been increasing, and that the proportion of transactions paying something other than the standard fees has been increasing. However it’s also worth noting that the proportion of 3-input transactions using non-standard fees actually decreased in November — which likely indicates that many users (or the maintainers of wallet software used by many users) had simply increased the default fee temporarily while concerned about the stress test, and reverted to defaults when the concern subsided, rather than using a wallet that estimates fees dynamically. In any event, by November 2015, we have at least about a thousand transactions per day at each size, even after excluding standard fees.

If we focus on the sextiles that roughly converge to the trend line we used earlier, we can, in fact make a very interesting observation: after November 2015, there is significant harmonisation on fee levels across different transaction sizes, and that harmonisation remains fairly steady even as the fee level changes dynamically over time:

Observations this time?

• After November 2015, a large bunch of transactions of difference sizes were calculating fees on a per-byte basis, and tracking a common fee-per-byte level, which has both increased and decreased since then. That is to say, a significant number of transactions are using market-based fees!
• The current market rate is slightly lower than the what a 0.1 mBTC, 2-input, 2-output transaction is paying (ie, 0.27 mBTC/kB).
• The recent observed markets rate correspond roughly to the 12-minute or 20-minute fee rates in the bitcoinfees graph provided earlier. That is, paying higher rates than the observed market rates is unlikely to result in quicker confirmation.
• There are many transactions paying significantly higher rates (eg, 1-input 2-output transactions paying a flat 0.1 mBTC).
• There are also many transactions paying lower rates (eg, 3-input 2-output transactions paying a flat 0.1 mBTC) that can expect delayed confirmation.

Along with the trend line, I’ve added four grey, horizontal guide lines on those graphs; one at each of the standard fee rates for the transaction sizes we’re considering (0.1 mBTC/kB for 1000 byte transactions, 0.19 mBTC/kB for 520 byte transactions, 0.27 mBTC/kB for 370 byte transactions, and 0.45 mBTC/kB for 220 byte transactions).

An interesting fact to observe is that when the market rate goes above any of the grey dashed lines, then transactions of the corresponding size that just pay the standard 0.1 mBTC fee become now less profitable to mine than transactions that pay the fees at the market rate. In a very particular sense this will induce a “fee event”, of the type mentioned earlier. That is, with the fee rate above 0.1 mBTC/kB, transactions of around 1000 bytes that pay 0.1 mBTC will generally suffer delays. Following the graph, for the transactions we’re looking at there have already been two such events — a fee event in July 2015, where 1000 byte transactions paying standard fees began getting delayed regularly due to the market fees began exceeding 0.1 mBTC/kB (ie, the 0.1 mBTC fee divided by 1 kB transaction size); and following that a second fee event during November impacting 3-input, 2-output transactions, due to market fees exceeding 0.19 mBTC/kB (ie, 0.1 mBTC divided by 0.52 kB). Per the graph, a few of the trend lines are lingering around 0.27 mBTC/kB, indicating a third fee event is approaching, where 370 byte transactions (ie 2-input, 2-output) paying standard fees will start to suffer delayed confirmations.

However the grey lines can also be considered as providing “resistance” to fee increases — for the market rate to go above 0.27 mBTC/kB, there must be more transactions attempting to pay the market rate than there were 2-input, 2-output transactions paying 0.1 mBTC. And there were a lot of those — tens of thousands — which means market fees will only be able to increase with higher adoption of software that calculates fees using dynamic estimates.

It’s not clear to me why fees harmonised so effectively as of November; my best guess is that it’s just the result of gradually increasing adoption, accentuated by my choice of quantiles to look at, along with averaging those results over a fortnight. At any rate, most of the interesting activity seems to have taken place around August:

• Bitcoin Core 0.11.0 came out in July with some minor fee estimation improvements.
• Electrum came out with dynamic fees in 2.4.1 in August.
• Copay (by bitpay) adder dynamic fees in 1.1.3 in August.
• Mycelium added per-byte fees in 2.5.8 in December.

Of course, obviously many wallets still don’t do per-byte, dynamic fees as far as I can tell:

• Blockchain.info just defaults to 0.1 mBTC as far as I can tell, the API seems to require a minimum fee of 0.1 mBTC
• coinbase.com pays 0.3 mBTC per transaction (from what I’ve seen, they tend to use 3-input, 3-output transactions, which presumably means about 600 bytes per transaction for a rate of perhaps 0.5 mBTC/kB)
• Airbitz seems to choose a fee based on transaction amount rather than transaction size
• myTrezor seems have a default 0.1 mBTC fee, that can optionally be raised to 0.5 mBTC
• bitcoinj does not do per-byte fees, or calculate fees dynamically (although an app based on bitcoinj might do so)

Summary

• Many wallets still don’t calculate fees dynamically, or even calculate fees at a per-byte level.
• A significant number of wallets are dynamically calculating fees, at a per-byte granularity
• Wallets that dynamically calculate fees pay substantially lower fees than those that don’t
• Paying higher than dynamically calculated market rates generally will not get your transaction confirmed any quicker
• Market-driven fees have risen to about the same fee level that wallets used for 2-input, 2-output transactions at the start of 2015
• Market-driven fees will only be able to rise further with increased adoption of wallets that support market-driven fees.
• There have been two fee events for wallets that don’t do market based fees, and paid a flat fee of 0.1 mBTC already. For those wallets, since about July 2015, fees have been high enough to cause transactions near 1000 bytes to have delayed confirmations; and since about November 2015, fees have been high enough to cause transactions above 520 bytes (ie, 3-input, 2-output) to be delayed. A third fee event is very close, affecting transactions above 370 bytes (ie, 2-input, 2-output).

Prior to Christmas, Rusty did an interesting post on bitcoin fees which I thought warranted more investigation. My first go involved some python parsing of bitcoin-cli results; which was slow, and as it turned out inaccurate — bitcoin-cli returns figures denominated in bitcoin with 8 digits after the decimal point, and python happily rounds that off, making me think a bunch of transactions that paid 0.0001 BTC in fees were paying 0.00009999 BTC in fees. Embarrassing. Anyway, switching to bitcoin-iterate and working in satoshis instead of bitcoin just as Rusty did was a massive improvement.

From a miner’s perspective (ie, the people who run the computers that make bitcoin secure), fees are largely irrelevant — they’re receiving around $11000 USD every ten minutes in inflation subsidy, versus around $80 USD in fees. If that dropped to zero, it really wouldn’t make a difference. However, in around six months the inflation subsidy will halve to 12.5 BTC; which, if the value of bitcoin doesn’t rise enough to compensate, may mean miners will start looking to turn fee income into real money — earning $5500 in subsidy plus $800 from fees could be a plausible scenario, eg (though even that doesn’t seem likely any time soon).

Even so, miners don’t ignore fees entirely even now — they use fees to choose how to fill up about 95% of each block (with the other 5% filled up more or less according to how old the bitcoins being spent are). In theory, that’s the economically rational thing to do, and if the theory pans out, miners will keep doing that when they start trying to get real income from fees rather than relying almost entirely on the inflation subsidy. There’s one caveat though: since different transactions are different sizes, fees are divided by the transaction size to give the fee-per-kilobyte before being compared. If you graph the fee paid by each kB in a block you thus get a fairly standard sort of result — here’s a graph of a block from a year ago, with the first 50kB (the priority area) highlighted:

You can see a clear overarching trend where the fee rate starts off high and gradually decreases, with two exceptions: first, the first 50kB (shaded in green) has much lower fees due to mining by priority; and second, there are frequent short spikes of high fees, which are likely produced by high fee transactions that spend the coins mined in the preceeding transaction — ie, if they had been put any earlier in the block, they would have been invalid. Equally, compared to the priority of the first 50kB of transactions, the the remaining almost 700kB contributes very little in terms of priority.

But, as it turns out, bitcoin wallet software often pretty much just tends to pick a particular fee and use it for all transactions no matter the size:

From the left hand graph you can see that, a year ago, wallet software was mostly paying about 10000 satoshi in fees, with a significant minority paying 50000 satoshi in fees — but since those were at the end of the block, which was ordered by satoshis per byte, those transactions were much bigger, so that their fee/kB was lower. This seems to be due to some shady maths: while the straightforward way of doing things would be to have a per-byte fee and multiply that by the transaction’s size in bytes, eg 10 satoshis/byte * 233 bytes gives 2330 satoshi fee; things are done in kilobytes instead, and a rounding mistake occurs, so rather than calculating 10000 satoshis/kilobyte * 0.233 kilobytes, the 0.233 is rounded up to 1kB first, and the result is just 10000 satoshi. The second graph reverses the maths to work out what the fee/kilobyte (or part thereof) figure would have been if this formula was used, and for this particular block, pretty much all the transactions look how you’d expect if exactly that formula was used.

As a reality check, 1 BTC was trading at about $210 USD at that time, so 10000 satoshi was worth about 2.1c at the time; the most expensive transaction in that block, which goes off the scale I’ve used, spent 240000 satoshi in fees, which cost about 50c.

Based on this understanding, we can look back through time to see how this has evolved — and in particular, if this formula and a few common fee levels explain most transactions. And it turns out that they do:

The first graph is essentially the raw data — how many of each sort of fee made it through per day; but it’s not very helpful because bitcoin’s grown substantially. Hence the second graph, which just uses the smoothed data and provides the values in percentage terms stacked one on top of the other. That way the coloured area lets you do a rough visual comparison of the proportion of transactions at each “standard” fee level.

In fact, you can break up that graph into a handful of phases where there is a fairly clear and sudden state change between each phase, while the distribution of fees used for transactions during that phase stays relatively stable:

That is:

1. in the first phase, up until about July 2011, fees were just getting introduced and most people paid nothing; fees began at 1,000,000 satoshi (0.01 BTC) (v 0.3.21) before setting on a fee level of 50000 satoshi per transaction (0.3.23).
2. in the second phase, up until about May 2012, maybe 40% of transactions paid 50000 satoshi per transaction, and almost everyone else didn’t pay anything
3. in the third phase, up until about November 2012, close to 80% of transactions paid 50000 satoshi per transaction, with free transactions falling to about 20%.
4. in the fourth phase, up until July 2013, free transactions continue to drop, however fee paying transactions split about half and half between paying 50000 satoshi and 100000 satoshi. It looks to me like there was an option somewhere to double the default fee in order to get confirmed faster (which also explains the 20000 satoshi fees in future phases)
5. in the fifth phase, up until November 2013, the 100k satoshi fees started dropping off, and 10k satoshi fees started taking over (v 0.8.3)
6. in the sixth phase, the year up to November 2014, transactions paying fees of 50k and 100k and free transactions pretty much disappeared, leaving 75% of transactions paying 10k satoshi, and maybe 15% or 20% of transactions paying double that at 20k satoshi.
7. in the seventh phase, up until July 2015, pretty much everyone using standard fees had settled on 10k satoshi, but an increasing number of transactions started using non-standard fees, presumably variably chosen based on market conditions (v 0.10.0)
8. in the eighth phase, up until now, things go a bit haywire. What I think happened is the “stress tests” in July and September caused the number of transactions with variable fees to spike substantially, which caused some delays and a lot of panic, and that in turn caused people to switch from 10k to higher fees (including 20k), as well as adopt variable fee estimation policies. However over time, it looks like the proportion of 10k transactions has crept back up, presumably as people remove the higher fees they’d set by hand during the stress tests.

Okay, apparently that was part one. The next part will take a closer look at the behaviour of transactions paying non-standard fees over the past year, in particular to see if there’s any responsiveness to market conditions — ie prices rising when there’s contention, or dropping when there’s not.

I’ve been intrigued by micropayments for, like, ever, so I’ve been following Rusty’s experiments with bitcoin with interest. Bitcoin itself, of course, has a roughly 10 minute delay, and a fee of effectively about 3c per transaction (or $3.50 if you count inflation/mining rewards) so isn’t really suitable for true microtransactions; but pettycoin was going to be faster and cheaper until it got torpedoed by sidechains, and more recently the lightning network offers the prospect of small payments that are effectively instant, and have fees that scale linearly with the amount (so if a $10 transaction costs 3c like in bitcoin, a 10c transaction will only cost 0.03c).

(Why do I think that’s cool? I’d like to be able to charge anyone who emails me 1c, and make $130/month just from the spam I get. Or you could have a 10c signup fee for webservice trials to limit spam but not have to tie everything to your facebook account or undergo turing trials. You could have an open wifi access point, that people don’t have to register against, and just bill them per MB. You could maybe do the same with tor nodes. Or you could setup bittorrent so that in order to receive a block I pay maybe 0.2c/MB to whoever sent it to me, and I charge 0.2c/MB to anyone who wants a block from me — leechers paying while seeders earn a profit would be fascinating. It’d mean you could setup a webstore to sell apps or books without having to sell your sell your soul to a corporate giant like Apple, Google, Paypal, Amazon, Visa or Mastercard. I’m sure there’s other fun ideas)

A bit over a year ago I critiqued sky-high predictions of bitcoin valuations on the basis that “I think you’d start hitting practical limitations trying to put 75% of the world’s transactions through a single ledger (ie hitting bandwidth, storage and processing constraints)” — which is currently playing out as “OMG the block size is too small” debates. But the cool thing about lightning is that it lets you avoid that problem entirely; hundreds, thousands or millions of transactions over weeks or years can be summarised in just a handful of transactions on the blockchain.

(How does lightning do that? It sets up a mesh network of “channels” between everyone, and provides a way of determining a route via those channels between any two people. Each individual channel is between two people, and each channel is funded with a particular amount of bitcoin, which is split between the two people in whatever way. When you route a payment across a channel, the amount of that payment’s bitcoins moves from one side of the channel to the other, in the direction of the payment. The amount of bitcoins in a channel doesn’t change, but when you receive a payment, the amount of bitcoins on your side of your channels does. When you simply forward a payment, you get more money in one channel, and less in another by the same amount (or less a small handling fee). Some bitcoin-based crypto-magic ensues to ensure you can’t steal money, and that the original payer gets a “receipt”. The end result is that the only bitcoin transactions that need to happen are to open a channel, close a channel, or change the total amount of bitcoin in a channel. Rusty gave a pretty good interview with the “Let’s talk bitcoin” podcast if the handwaving here wasn’t enough background)

Of course, this doesn’t work very well if you’re only spending money: it doesn’t take long for all the bitcoins on your lightning channels to end up on the other side, and at that point you can’t spend any more. If you only receive money over lightning, the reverse happens, and you’re still stuck just as quickly. It’s still marginally better than raw bitcoin, in that you have two bitcoin transactions to open and close a channel worth, say, $200, rather than forty bitcoin transactions, one for each $5 you spend on coffee. But that’s only a fairly minor improvement.

You could handwave that away by saying “oh, but once lightning takes off, you’ll get your salary paid in lightning anyway, and you’ll pay your rent in lightning, and it’ll all be circular, just money flowing around, lubricating the economy”. But I think that’s unrealistic in two ways: first, it won’t be that way to start with, and if things don’t work when lightning is only useful for a few things, it will never take off; and second, money doesn’t flow around the economy completely fluidly, it accumulates in some places (capitalism! profits!) and drains away from others. So it seems useful to have some way of making degenerate scenarios actually work — like someone who only uses lightning to spend money, or someone who receives money by lightning but only wants to spend cold hard cash.

One way you can do that is if you imagine there’s someone on the lightning network who’ll act as an exchange — who’ll send you some bitcoin over lightning if you send them some cash from your bank account, or who’ll deposit some cash in your bank account when you send them bitcoins over lightning. That seems like a pretty simple and realistic scenario to me, and it makes a pretty big improvement.

I did a simulation to see just how well that actually works out. With “Alice” as a coffee consumer, who does nothing with lightning but buy $5 espressos from “Emma” and refill her lightning wallet by exchanging cash with “Xavier” who runs an exchange, converting dollars (or gold or shares etc) to lightning funds. Bob, Carol and Dave run lightning nodes and take a 1% cut of any transactions they forward. I uploaded a video to youtube that I think helps visualise the payment flows and channel states (there’s no sound):

It starts off with Alice and Xavier putting $200 in channels in the network; Bob, Carol and Dave putting in $600 each, and Emma just waiting for cash to arrive. The statistics box in the top right tracks how much each player has on the lightning network (“ln”), how much profit they’ve made (“pf”), and how many coffees Alice has ordered from Emma. About 3000 coffees later, it ends up with Alice having spent about $15,750 in real money on coffee ($5.05/coffee), Emma having about $15,350 in her bank account from making Alice’s coffees ($4.92/coffee), and Bob, Carol and Dave having collectively made about $400 profit on their $1800 investment (about 22%, or the $0.13/coffee difference between what Alice paid and Emma received). At that point, though, Bob, Carol and Dave have pretty much all the funds in the lightning network, and since they only forward transactions but never initiate them, the simulation grinds to a halt.

You could imagine a few ways of keeping the simulation going: Xavier could refresh his channels with another $200 via a blockchain transaction, for instance. Or Bob, Carol and Dave could buy coffees from Emma with their profits. Or Bob, Carol and Dave could cash some of their profits out via Xavier. Or maybe they buy some furniture from Alice. Basically, whatever happens, you end up relying on “other economic activity” happening either within lightning itself, or in bitcoin, or in regular cash.

But grinding to a halt after earning 22% and spending/receiving $15k isn’t actually too bad even as it is. So as a first pass, it seems like a pretty promising indicator that lightning might be feasible economically, as well as technically.

One somewhat interesting effect is that the profits don’t get distributed particularly evenly — Bob, Carol and Dave each invest $600 initially, but make $155.50 (25.9%), $184.70 (30.7%) and $52.20 (8.7%) respectively. I think that’s mostly a result of how I chose to route payments — it optimises the route to choose channels with the most funds in order to avoid payments getting stuck, and Dave just ends up handling less transaction volume. Having a better routing algorithm (that optimises based on minimum fees, and relies on channel fees increasing when they become unbalanced) might improve things here. Or it might not, and maybe Dave needs to quote lower fees in general or establish a channel with Xavier in order to bring his profits up to match Bob and Carol.

At Bradley Kuhn’s talk at linux.conf.au this year, I was surprised and disappointed to see a slide quoting some FUD (in the traditional Fear-Uncertainty-Doubt model, a la the Microsoft Halloween documents from back in the day) about the GPL and the SFLC’s enforcement thereof. Here’s the quote:

This is not just a theoretical concern. As aggressively as the BSA protects the interests of its commercial members, [GPL enforcers] protect the GPL license in high-profile lawsuits against large corporations. [FSF] writes about their expansion of “active license enforcement”. So the cost of compliance with copyleft code can be even greater than the use of proprietary software, since an organization risks being forced to make the source code for their proprietary product public and available for anyone to use, free of charge. […]

The Apache Advantage

However, not all open source licenses are copyleft license. A subset of open source licenses, generally called “permissive” licenses, are much more friendly for corporate use.

The quote/slide is available at about 20m into Bradley’s talk. A quick google reveals the source of this as a page from openoffice.org which is, indeed, an Apache project. The revision history for that page is available via subversion.

The elisions in Bradley’s quote changed “the Software Freedom Law Centre” (Bradley’s employer) to “GPL enforcers”, simplified the reference to the FSF, and dropped off a couple of sentences of qualification:

To mitigate this risk requires more employee education, more approval cycles, more internal audits and more worries. This is the increased cost of compliance when copyleft software is brought into an organization. This is not necessarily a bad thing. It is just the reality of using open source software under these licenses, and must be weighed in considered as one cost-driver among many.

I don’t really think any of that changes Bradley’s point: the Apache Foundation is really saying that the GPL and the SFLC is worse than the BSA and proprietary licenses.

After getting home from LCA, I thought it was worth writing to the Apache Foundation about this. I tried twice, on 22nd January and again on 1st February. I didn’t receive any response.

From: Anthony Towns

I was at Bradley Kuhn’s talk at linux.conf.au 2015 last week, and was struck by a quote he attributed to the Apache Software Foundation which compared the SFLC’s efforts to enforce GPL compliance with the BSA’s campaigns on software piracy, and then went on to call the SFLC worse. The remarks and slide can be found at approximately the 20 minute mark in the recording on youtube:

www.youtube.com/watch?v=-ItFjEG3LaA#t=19m52s

Doing a google search for the quote, I found a hit on the Apache OpenOffice.org website:

http://www.openoffice.org/why/why_compliance.html

which although it’s a (somewhat major) project rather than the apache site itself, doesn’t give any indication that it’s authored or authorised by someone other than the Apache Foundation.

I couldn’t find any indication via web.archive.org that that page predated Apache’s curation of the OpenOffice.org project (I wondered if it might have been something Oracle would write, rather than the Apache Foundation).​ Doing some more searching, I found a svn log that seems to indicate it’s primarily authored by Rob Weir with minor edits by Andrea Pescetti (who I understand is the VP for Apache OpenOffice):

​http://svn.apache.org/viewvc/openoffice/ooo-site/trunk/content/why/why_compliance.mdtext?view=log

Is this really an accurate representation of the Apache Foundation’s current stance on copyleft licenses, the GPL and the SFLC’s enforcement efforts?

Apparently we now live in a world where Microsoft happily releases GPL-licensed software, while the Apache Foundation happily spreads FUD against it.

Bitcoincerns — as in Bitcoin concerns! Get it? Hahaha.

Despite having an interest in ecash, I haven’t invested in any bitcoins. I haven’t thought about it any depth, but my intuition says I don’t really trust it. I’m not really sure why, so I thought I’d write about it to see if I could come up with some answers.

The first thing about bitcoin that bothered me when I first heard about it was the concept of burning CPU cycles for cash — ie, setup a bitcoin miner, get bitcoins, …, profit. The idea of making money by running calculations that don’t provide any benefit to anyone is actually kind of offensive IMO. That’s one of the reasons I didn’t like Microsoft’s Hashcash back in the day. I think that’s not actually correct, though, and that the calculations being run by miners are actually useful in that they ensure the validity of bitcoin transfers.

I’m not particularly bothered by the deflationary expectations people have of bitcoin. The “wild success” cases I’ve seen for bitcoin estimate their value by handy wavy arguments where you take a crazy big number, divide it by the 20M max bitcoins that are available, and end up with a crazy big number per bitcoin. Here’s the argument I’d make: someday many transactions will take place purely online using bitcoin, let’s say 75% of all transactions in the world by value. Gross World Product (GDP globally) is $40T, so 75% of that is $30T per year. With bitcoin, each coin can participate in a transaction every ten minutes, so that’s up to about 52,000 transactions a year, and there are up to 20M bitcoins. So if each bitcoin is active 100% of the time, you’d end up with a GWP of 1.04T bitcoins per year, and an exchange rate of $28 per bitcoin, growing with world GDP. If, despite accounting for 75% of all transactions, each bitcoin is only active once an hour, multiply that figure by six for $168 per bitcoin.

That assumes bitcoins are used entirely as a medium of exchange, rather than hoarded as a store of value. If bitcoins got so expensive that they can only just represent a single Vietnamese Dong, then 21,107 “satoshi” would be worth $1 USD, and a single bitcoin would be worth $4737 USD. You’d then only need 739k bitcoins each participating in a transaction once an hour to take care of 75% of the world’s transactions, with the remaining 19M bitcoins acting as a value store worth about $91B. In the grand scheme of things, that’s not really very much money. I think if you made bitcoins much more expensive than that you’d start cutting into the proportion of the world’s transactions that you can actually account for, which would start forcing you to use other cryptocurrencies for microtransactions, eg.

Ultimately, I think you’d start hitting practical limitations trying to put 75% of the world’s transactions through a single ledger (ie hitting bandwidth, storage and processing constraints), and for bitcoin, that would mean having alternate ledgers which is equivalent to alternate currencies. That would involve some tradeoffs — for bitcoin-like cryptocurrencies you’d have to account for how volatile alternative currencies are, and how amenable the blockchains are to compromise, but, provided there are trusted online exchanges to convert one cryptocurrency into another, that’s probably about it. Alternate cryptocurrencies place additional constraints on the maximum value of bitcoin itself, by reducing the maximum amount of GWP happening in bitcoin versus other currencies.

It’s not clear to me how much value bitcoin has as a value store. Compared to precious metals, is much easier to transport, much easier to access, much less expensive to store and secure. On the other hand, it’s much easier to destroy or steal. It’s currently also very volatile. As a store of value, the only things that would make it better or worse than an alternative cryptocurrency are (a) how volatile it is, (b) how easy it is to exchange for other goods (liquidity), and (c) how secure the blockchain/algorithms/etc are. Of those, volatility seems like the biggest sticking point. I don’t think it’s unrealistic to imagine wanting to store, say, $1T in cryptocurrency (rather than gold bullion, say), but with only 20M bitcoins, that would mean each bitcoin was worth at least $50,000. Given a current price of about $500, that’s a long way away — and since there are a lot of things that could happen in the meantime, I think high volatility at present is a pretty plausible outcome.

I’m not sure if it’s possible or not, but I have to wonder if a bitcoin based cryptocurrency designed to be resistant to volatility would be implementable. I’m thinking (a) a funded exchange guaranteeing a minimum exchange rate for the currency, and (b) a maximum number of coins and coin generation rate for miners that makes that exchange plausible. The exchange for, let’s call it “bitbullion”, should self-fund to some extent by selling new bitbullion at a price of 10% above guidance, and buying at a price of 10% below guidance (and adjusting guidance up or down slightly any time it buys or sells, purely in order to stay solvent).

I don’t know what the crypto underlying the bitcoin blockchain actually is. I’m surprised it’s held up long enough to get to where bitcoin already is, frankly. There’s nominally $6B worth of bitcoins out there, so it would seem like you could make a reasonable profit if you could hack the algorithm. If there were hundreds of billions or trillions of dollars worth of value stored in cryptocurrency, that would be an even greater risk: being able to steal $1B would tempt a lot of people, being able to destroy $100B, especially if you could pick your target, would tempt a bunch more.

So in any event, the economic/deflation concerns seem assailable to me. The volatility not so much, but I’m not looking to replace my bank at the moment, so that doesn’t bother me either.

I’m very skeptical about the origins of bitcoin. The fact it’s the first successful cryptocurrency, and also the first definitively non-anonymous one is pretty intriguing in my book. Previous cryptocurrencies like Chaum’s ecash focussed on allowing Alice to pay Bob $1 without there being a record of anything other than Alice is $1 poorer, and Bob is $1 richer. Bitcoin does exactly the opposite, providing nothing more than a globally verifiable record of who paid whom how much at what time. That seems like a dream come true for law enforcement — you don’t even have to get a warrant to review the transactions for an account, because everyone’s accounts are already completely public. Of course, you still have to find some way to associate a bitcoin wallet id with an actual person, but I suspect that’s a challenge with any possible cryptocurrency. I’m not quite sure what the status of the digicash/ecash patents are/were, but they were due to expire sometime around now (give or take a few years), I think.

The second thing that strikes me as odd about bitcoin is how easily it’s avoided being regulated to death. I had expected the SEC to decide that bitcoins are a commodity with no real difference to a share certificate, and that as a consequence they can only be traded using regulated exchanges by financial professionals, or similar. Even if bitcoins still count as new enough to only have gotten a knee-jerk regulatory response rather than a considered one (with at $500 a pop and significant mainstream media coverage, I doubt), I would have expected something more along the lines of “bitcoin trading is likely to come under regulation XYZ, operating or using an unregulated exchange is likely to be a crime, contact a lawyer” rather than “we’re looking into it”. That makes it seem like bitcoin has influential friends who aren’t being very vocal in public, and conspiracy theories involving NSA and CIA/FBI folks suggesting leaving bitcoin alone for now might help fight crime, seem more plausible than ones involving Gates or Soros or someone secretly creating a new financial world order.

The other aspect is that it seems like there’s only really four plausible creators of bitcoin: one or more super smart academic types, a private startup of some sort, an intelligence agency, or a criminal outfit. It seems unlikely to me that a criminal outfit would create a cryptocurrency with a strong audit trail, but I guess you never know. It seems massively unlikely that a legitimate private company would still be secret, rather than cashing out. Likewise it seems unlikely that people who’d just done it because it seemed like an interesting idea would manage to remain anonymous still; though that said, cryptogeeks are weird like that.

If it was created by an intelligence agency, then its life to date makes some sense: advertise it as anonymous online cash that’s great for illegal stuff like buying drugs and can’t be tracked, sucker in a bunch of criminals to using it, then catch them, confiscate the money, and follow the audit trail to catch more folks. If that’s only worked for silk road folks, that’s probably pretty small-time. If bitcoin was successfully marketed as “anonymous, secure cryptocurrency” to organised crime or terrorists, and that gave you another angle to attack some of those networks, you could be on to something. It doesn’t seem like it would be difficult to either break into MtGox and other trading sites to gain an initial mapping between bitcoins and real identities, or to analyse the blockchain comprehensively enough to see through most attempts at bitcoin laundering.

Not that I actually have a problem with any of that. And honestly, if secret government agencies lean on other secret government agencies in order to create an effective and efficient online currency to fight crime, that’s probable a win-win as far as I’m concerned. One concern I guess I have though, is that if you assume a bunch of law-enforcement cryptonerds build bitcoin, is that they might also have a way of “turning it off” — perhaps a real compromise in the crypto that means they can easily create forks of the blockchain and make bitcoins useless, or just enough processor power that they can break it by bruteforce, or even just some partial results in how to break bitcoin that would destroy confidence in it, and destroy the value of any bitcoins. It’d be fairly risky to know of such a flaw, and trust that it wouldn’t be uncovered by the public crypto research community, though.

All that said, if you ignore the criminal and megalomaniacal ideas for bitcoin, and assume the crypto’s sound, it’s pretty interesting. At the moment, a satoshi is worth 5/10,000ths of a cent, which would be awesome for microtransactions if the transaction fee wasn’t at 5c. Hmm, looks like dogecoin probably has the right settings for microtransactions to work. Maybe I should have another go at the pay-per-byte wireless capping I was thinking of that one time… Apart from microtransactions, some of the conditional/multiparty transaction possibilities are probably pretty interesting too.

I’ve been doing a bit of playing around with REST APIs lately, both at work and for my own amusement. One of the things that was frustrating me a bit was that actually accessing the APIs was pretty baroque — you’d have to construct urls manually with string operations, manually encode any URL parameters or POST data, then pass that to a requests call with params to specify auth and SSL validation options and possibly cookies, and then parse whatever response you get to work out if there’s an error and to get at any data. Not a great look, especially compared to XML-RPC support in python, which is what REST APIs are meant to obsolete. Compare, eg:

server = xmlrpclib.Server("http://foo/XML-RPC")
print server.some.function(1,2,3,{"foo": "bar"})

with:

base_url = "https://api.github.com/"
resp = requests.get(base_url + "/repos/django/django")
if resp.ok:
    res = resp.json()
else:
    raise Exception(r.json())

That’s not to say the python was is bad or anything — it’s certainly easier than trying to do it in shell, or with urllib2 or whatever. But I like using python because it makes the difference between pseudocode and real code small, and in this case, the xmlrpc approach is much closer to the pseudocode I’d write than the requests code.

So I had a look around to see if there were any nice libraries to make REST API access easy from the client side. Ended up getting kind of distracted by reading through various arguments that the sorts of things generally called REST APIs aren’t actually “REST” at all according to the original definition of the term, which was to describe the architecture of the web as a whole. One article that gives a reasonably brief overview is this take on REST maturity levels. Otherwise doing a search for the ridiculous acronym “HATEOAS” probably works. I did some stream-of-consciousness posts on Google-Plus as well, see here, here and here.

The end result was I wrote something myself, which I called beanbag. I even got to do it mostly on work time and release it under the GPL. I think it’s pretty cool:

github = beanbag.BeanBag("https://api.github.com")
x = github.repos.django.django()
print x["name"]

As per the README in the source, you can throw in a session object to do various sorts of authentication, including Kerberos and OAuth 1.0a. I’ve tried it with github, twitter, and xero’s public APIs with decent success. It also seems to work with Magento and some of Red Hat’s internal tools without any hassle.

Two posts in one month! Woah!

A couple of weeks ago there was a flurry of stuff about the Liberal party’s Parental Leave policy (viz: 26 weeks at 100% of your wage, paid out of the general tax pool rather than by your employer, up to $150k), mostly due to a coalition backbencher coming out against it in the press (I’m sorry, I mean, due to “an internal revolt”, against a policy “detested by many in the Coalition”). Anyway, I haven’t had much cause to give it any thought beforehand — it’s been a policy since the 2010 election I think; but it seems like it might have some interesting consequences, beyond just being more money to a particular interest group.

In particular, one of the things that doesn’t seem to me to get enough play in the whole “women are underpaid” part of the ongoing feminist, women-in-the-workforce revolution, is how much both the physical demands of pregnancy and being a primary caregiver justifiably diminish the contributions someone can make in a career. That shouldn’t count just the direct factors (being physically unable to work for a few weeks around birth, and taking a year or five off from working to take care of one or more toddlers, eg), but the less direct ones like being less able to commit to being available for multi-year projects or similar. There’s also probably some impact from the cross-over between training for your career and the best years to get pregnant — if you’re not going to get pregnant, you just finish school, start working, get more experience, and get paid more in accordance with your skills and experience (in theory, etc). If you are going to get pregnant, you finish school, start working, get some experience, drop out of the workforce, watch your skills/experience become out of date, then have to work out how to start again, at a correspondingly lower wage — or just choose a relatively low skill industry in the first place, and accept the lower pay that goes along with that.

I don’t think either the baby bonus or the current Australian parental leave scheme has any affect on that, but I wonder if the Liberal’s Parental Leave scheme might.

There’s three directions in which it might make a difference, I think.

One is for women going back to work. Currently, unless your employer is more generous, you have a baby, take 16 weeks of maternity leave, and get given the minimum wage by the government. If that turns out to work for you, it’s a relatively easy decision to decide to continue being a stay at home mum, and drop out of the workforce for a while: all you lose is the minimum wage, so it’s not a much further step down. On the other hand, after spending half a year at your full wage, taking care of your new child full-time, it seems a much easier decision to go back to work than to be a full-time mum; otherwise you’ll have to deal with a potentially much lower family income at a time when you really could choose to go back to work. Of course, it might work out that daycare is too expensive, or that the cut in income is worth the benefits of a stay at home mum, but I’d expect to see a notable pickup in new mothers returning to the workforce around six months after giving birth anyway. That in turn ought to keep women’s skills more current, and correspondingly lift wages.

Another is for employers dealing with hiring women who might end up having kids. Dealing with the prospect of a likely six-month unpaid sabbatical seems a lot easier than dealing with a valued employee quitting the workforce entirely on its own, but it seems to me like having, essentially, nationally guaranteed salary insurance in the event of pregnancy would make it workable for the employee to simply quit, and just look for a new job in six month’s time. And dealing with the prospect of an employee quitting seems like something employers should expect to have to deal with whoever they hire anyway. Women in their 20s and 30s would still have the disadvantage that they’d be more likely to “quit” or “take a sabbatical” than men of the same age and skillset, but I’m not actually sure it would be much more likely in that age bracket. So I think there’s a good chance there’d be a notable improvement here too, perhaps even to the point of practical equality.

Finally, and possibly most interestingly, there’s the impact on women’s expectations themselves. One is that if you expect to be a mum “real soon now”, you might not be pushing too hard on your career, on the basis that you’re about to give it up (even if only temporarily) anyway. So, not worrying about pushing for pay rises, not looking for a better job, etc. It might turn out to be a mistake, if you end up not finding the right guy, or not being able to get pregnant, or something else, but it’s not a bad decision if you meet your expectations: all that effort on your career for just a few weeks pay off and then you’re on minimum wage and staying home all day. But with a payment based on your salary, the effort put into your career at least gives you six month’s worth of return during motherhood, so it becomes at least a plausible investment whether or not you actually become a mum “real soon now” or not.

According to the 2010 tax return stats I used for my previous post, the gender gap is pretty significant: there’s almost 20% less women working (4 million versus 5 million), and the average working woman’s income is more than 25% less than the average working man’s ($52,600 versus $71,500). I’m sure there are better ways to do the statistics, etc, but just on those figures, if the female portion of the workforce was as skilled and valued as the male portion, you’d get a $77 billion dollar increase in GDP — if you take 34% as the proportion of that that the government takes, it would be a $26 billion improvement to the budget bottom line. That, of course, assumes that women would end up no more or less likely to work part time jobs than men currently are; that seems unlikely to me — I suspect the best that you’d get is that fathers would become more likely to work part-time and mothers less likely, until they hit about the same level. But that would result in a lower increase in GDP. Based on the above arguments, there would be increase the number of women in the workforce as well, though that would get into confusing tradeoffs pretty quickly — how many families would decide that a working mum and stay at home dad made more sense than a stay at home mum and working dad, or a two income family; how many jobs would be daycare jobs (counted as GDP) in place of formerly stay at home mums (not counted as GDP, despite providing similar value, but not taxed either), etc.

I’m somewhat surprised I haven’t seen any support for the coalition’s plans along these lines anywhere. Not entirely surprised, because it’s the sort of argument that you’d make from the left — either as a feminist, anti-traditional-values, anti-stay-at-home-mum plot for a new progressive genderblind society; or from a pure technocratic economic point-of-view; and I don’t think I’ve yet seen anyone with lefty views say anything that might be construed as being supportive of Tony Abbott… But I would’ve thought someone on the right Bolt or Albrechtsen or Australia’s leading libertarian and centre-right blog or the Liberal party’s policy paper might have canvassed some of the other possible pros to the idea rather than just worrying about the benefits to the recipients, and how it gets paid for. In particular, the argument for any sort of payment like this shouldn’t be about whether it’s needed/wanted by the recipient, but how it benefits the rest of society. Anyway.

It’s been too long since I did an economics blog post…

Way back when, I wrote fairly approvingly of the recommendations to simplify the income tax system. The idea being to more or less keep charging everyone the same tax rate, but to simplify the formulae from five different tax rates, a medicare levy, and a gradually disappearing low-income tax offset, to just a couple of different rates (one kicking in at $25k pa, one at $180k pa). The government’s adopted that in a half-hearted way — raising the tax free threshold to $18,200 instead of $25,000, and reducing but not eliminating the low-income tax offset. There’s still the medicare levy with its weird phase-in procedure, and there’s still four different tax rates. And there’s still all sorts of other deductions etc to keep people busy around tax time.

Anyway, yesterday I finally found out that the ATO publishes some statistics on how many people there are at various taxable income levels — table 9 of the 2009-2010 stats are the best I found, anyway. With that information, you can actually mess around with the tax rules and see what affect it actually has on government revenue. Or at least what it would have if there’d been no growth since 2010.

Anyway, by my calculations, the 2011-2012 tax rates would have resulted in about $120.7B of revenue for the government, which roughly matches what they actually reported receiving in that table ($120.3B). I think putting the $400M difference (or about $50 per taxpayer) down to deductions for dependants and similar that I’ve ignored seems reasonable enough. So going from there, if you followed the Henry review’s recommendations, dropping the Medicare levy (but not the Medicare surcharge) and low income tax offset, the government would end up with $117.41B instead, so about $3.3B less. The actual changes between 2011-2012 and 2012-2013 (reducing the LITO and upping the tax free threshold) result in $118.26B, which would have only been $2.4B less. Given there’s apparently a $12B fudge-factor between prediction and reality anyway, it seems a shame they didn’t follow the full recommendations and actually make things simpler.

Anyway, upping the Medicare levy by 0.5% seems to be the latest idea. By my count doing that and keeping the 2012-2013 rates otherwise the same would result in $120.90B, ie back to the same revenue as the 2011-2012 rates (though biased a little more to folks on taxable incomes of $30k plus, I think).

Personally, I think that’s a bit nuts — the medicare levy should just be incorporated into the overall tax rates and otherwise dropped, IMO, not tweaked around. And it’s not actually very hard to come up with a variation on the Henry review’s rates that both simplify tax levels, don’t increase tax on any individual by very much, and do increase revenue. My proposal would be: drop the medicare levy and low income tax offset entirely (though not the medicare levy surcharge or the deductions for dependants etc), and set the rates as: 35% for earnings above $25k, 40% for earnings above $80k, and 46.5% for earnings above $180k. That would provide government revenue of $120.92B, which is close enough to the same as the NDIS levy. It would cap the additional tax any individual pays to $2000 compared to 2012-13 rates, ie it wouldn’t increase the top marginal rate. It would decrease the tax burden on people with taxable incomes below $33,000 pa — the biggest winners would be people earning $25,000 who’d go from paying $1200 tax per year to nothing. The “middle class” earners between $35,000 and $80,000 would pay an extra $400-$500; higher income earners between $80,000 and $180,000 get hit between $500 and $2000, and anyone above $180,000 pays an extra $2,000. Everyone earning over about $34,000 but under about $400,000 would pay more tax than if the NDIS were just increased, everyone earning between $18,000 and $34,000 would be better off.

On a dollar basis, the comparison looks like:

Translating that to a percentage of income, it looks like:

Not pleasant, I’m sure, on the dual-$80k families in western Sydney who are just-scraping buy and all, but I don’t think it’s crazy unreasonable.

But the real win comes when you look at the marginal rates:

Rather than seven levels of marginal rate, there’s just three; and none of them are regressive — ie, you stop having cases like someone earning $30,000 paying 21% on their additional dollar of income versus someone earning $22,000 paying 29% on their extra dollar. At least philosophically and theoretically that’s a good thing. In practice, I’m not sure how much of a difference it makes:

There’s spikes at both the $80,000 and $35,000 points which involve 8% and 15% increases in the nominal tax rates respectively, which I think is mostly due to people transferring passive income to family members who either don’t work or have lower paid jobs — if you earn a $90,000 salary better to assign the $20,000 rental income from your units to your kid at uni and pay 15% or 30% tax on it, than assign it to yourself and pay 38%, especially if you then just deposit it back into your family trust fund either way. The more interesting spikes are those around the $20,000 and $30,000 points, but I don’t really understand why those are shaped the way they are, and couldn’t really be sure that they’d smooth out given a simpler set of marginal rates.

Anyway, I kind-of thought it was interesting that it’s not actually very hard to come up with a dramatically simpler set of tax rates, that’s both not overly punitive and gives about the same additional revenue as the mooted levy increase.

(As a postscript, I found it particularly interesting to see just how hard it is to get meaningful revenue increases by tweaking the top tax rate; there’s only about $33B being taxed at that rate, so you have to bump the rate by 3% to get a bump of $1B in overall revenue, which is either pretty punitive or pretty generous before you’re making any useful difference at all. I chose to leave it matching the current income level and rate; longer term, I think making the levels something like $25k, $100k, $200k, and getting the percentages to rounder figures (35%, 40%, 45%?) would probably be sensible. If I really had my druthers, I’d rather see the rate be 35% from $0-$100,000, and have the government distribute, say, $350 per fortnight to everyone — if you earn over $26k, that’s just the equivalent of a tax free threshold of $26k; if you don’t, it’s a helpful welfare payment, whether you’re a student, disabled, temporarily unemployed, retired, or something else like just wanting to take some time off to do charity work or build a business)

Okay, so it turns out an interesting, demanding, and rewarding job isn’t as compatible as I’d naively hoped with all the cool things I’d like to be doing as hobbies (like, you know, blogging more than once a year, or anything substantial at all…) Thinking it’s time to see if there’s any truth in the whole fitness fanatic thing of regular exercise helping…

Yikes. Been a while. I can’t think of anything intelligent to blog, so some linky tidbits instead:

• rpm 4.10 includes “~” as a special versioning character, just like dpkg has for ages. Holds a special place in my heart since I did the original patch for dpkg a bit over 11 years ago now. (And looking at that bug history now, it appears it was accepted for my birthday a year later, awww). “ls” from coreutils also supports it (they borrowed the code from dpkg, based on a copyright disclaimer request I’ve finally gotten around to replying to), though I don’t think it’s actually documented.

• Read a couple of interesting takes on the Facebook IPO: one from a “blue-collar hedge fund manager” (yeah, riiight), who blamed NASDAQ for not handling trades properly on opening day, then essentially forcing traders to sell their stock immediately to be compensated for trades not executed properly; and one from Nanex via ZeroHedge with an animation showing that NASDAQ was not actually making a market in Facebook stock for an extended period (claiming offers to buy for $43 and offers to sell for $42.99, but not executing them and clearing them out), screwing up the other exchanges they connect to and the high-frequency algorithmic traders that use them. To me, Google’s reverse-auction IPO that tried to ensure there wasn’t a day-one stock price “pop” just seems better all the time…

• Like I needed more reasons not to be impressed by US politics.

• SpaceX has been doing a pretty amazing demo: correctly handled launch abort, quick turn around on fix; successful launch; successful delivery of payload to the ISS. Get it back down again, and they’ve really got something. Also impressive: per Wikipedia at least, “As of May 2012, SpaceX has operated on total funding of approximately one billion dollars in its first ten years of operation”, 80% of which has come from payments by customers (“progress payments on long-term launch contracts and development contracts”). That is, about the same amount as what Facebook paid for Instagram and its 13 employees…

• Via Andrew Pollock’s g+ feed, Leap Motion looks nifty.

• I rode down to linux.conf.au in Ballarat this year — about 5000 kilometres of awesomeness. Here’s a photo from the way I took back, that I call “Hay, Hell and Booligal”:

  

Things are different now. That’s certain.

Or at least that’s what one of the marketing sites for my new employer has to say.

Back in March I started at Red Hat’s Brisbane office working in release engineering (or the “Release Configuration Management” team). Short summary: it’s been pretty fun so far.

Googling just now for something to link that provides some sort of context, I came upon a video with my boss (John Flanagan) and one of my colleagues (Jesse Keating) — neither of whom I’ve actually met yet — giving a talk to the ACM chapter at Northeastern University in Boston. (It’s an hour long, and doesn’t expect much background knowledge of Linux; but doesn’t go into anything in any great depth either)

My aim in deciding to go job hunting late last year was to get a large change of scenery and get to work with people who understood what I was doing — it eventually gets a bit old being a black box where computer problems go in, solutions come out, and you can only explain what happens in between with loose analogies before seeing eyes glaze over. Corporate environment, Fedora laptop, enterprise customers, and a zillion internal tools that are at least new to me, certainly counts as a pretty neat change of scenery; and I think I’ve now got about five layers of technical people between me and anyone who doesn’t have enough technical background to understand what I do on the customer side. Also, money appears in my bank account every couple of weeks, without having to send anyone a bill! It’s like magic!

The hiring process was a bit odd — mostly, I gather, because while I applied for an advertised position, the one I ended up getting was something that had been wanted for a while, but hadn’t actually had a request open. So I did a bunch of interviews for the job I was applying for, then got redirected to the other position, and did a few interviews for that without either me or the interviewers having a terribly clear idea what the position would involve. (I guess it didn’t really help that my first interview, which was to be with my boss’s boss, got rearranged because he couldn’t make it in due to water over the roads, and then Brisbane flooded; that the whole point of the position is that they didn’t have anyone working in that role closer than the Czech Republic is probably also a factor…)

As it’s turned out, that’s been a pretty accurate reflection of the role: I’ve mostly been setting my own priorities, which mostly means balancing between teaching myself how things work, helping out the rest of my team, and working with the bits of Red Hat that are local, or at least operate in compatible timezones. Happily, that seems to be working out fairly okay. (And at least the way I’ve been doing it isn’t much different to doing open source in general: “gah, this program is doing something odd. okay, find the source, see what it’s doing and why, and either (a) do something different to get what you want, or (b) fix the code. oh, and also, you now understand that program”)

As it turned out, that leads into the main culture shock I had on arriving: what most surprised me was actually the lack of differences compared to being involved in Debian — which admittedly might have been helped by a certain article hitting LWN just in time for my first day. “Ah, so that list is the equivalent of debian-devel. Good to know.” There’s a decent number of names that pop up that are familiar from Debian too, which is nice. Other comfortingly familiar first day activities were subscribing to more specific mailing lists, joining various IRC channels, getting my accounts setup and setting up my laptop. (Fedora was suggested, “not Debian” was recommended ;)

Not that everything’s the same — there’s rpm/yum versus dpkg/apt obviously, and there’s a whole morass of things to worry about working for a public company. But a lot of it fits into either “different to Debian, but not very” and “well, duh, Red Hat’s a for-profit, you have to do something like this, and that’s not a bad way of doing it”.

Hmm, not sure what else I can really talk about without at least running it by someone else to make sure it’s okay to talk about in public. I think there’s only a couple of things I’ve done so far that have gone via Fedora and are thus easy — the first was a quick python script to make publishing fedora torrents easier, and the other was a quick patch to the fedora buildsystem software to help support analytics. Not especially thrilling, though. I think Dennis is planning on throwing me into more Fedora stuff fairly soon, so hopefully that might change.