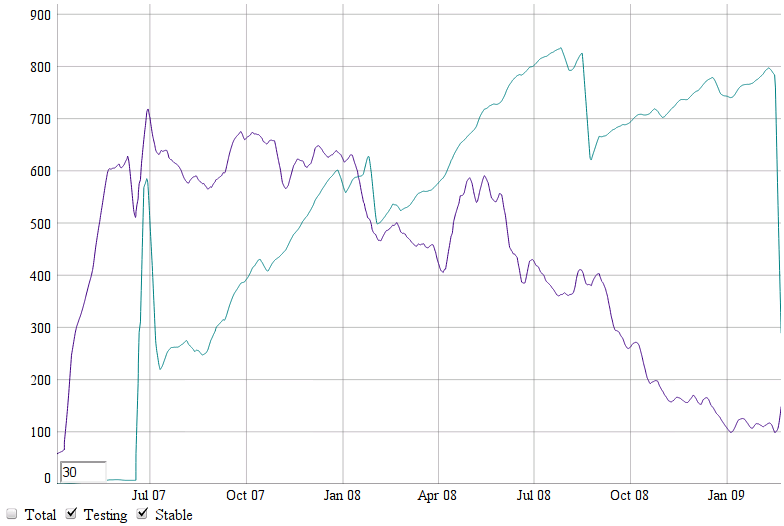
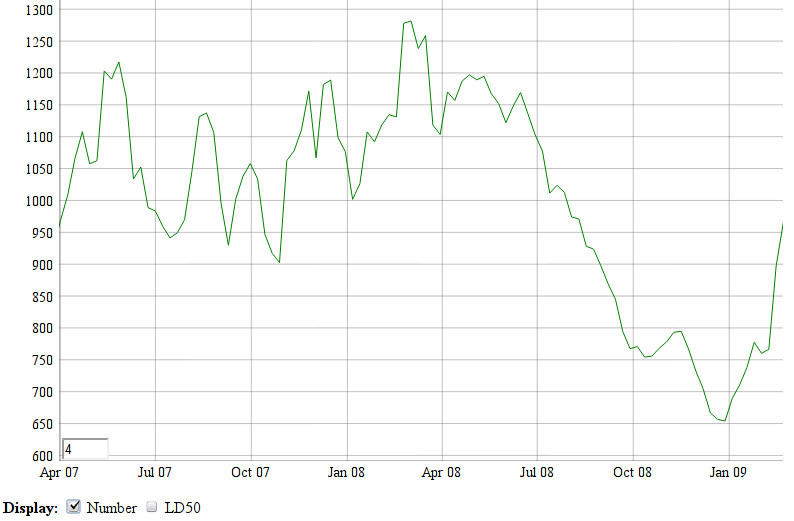
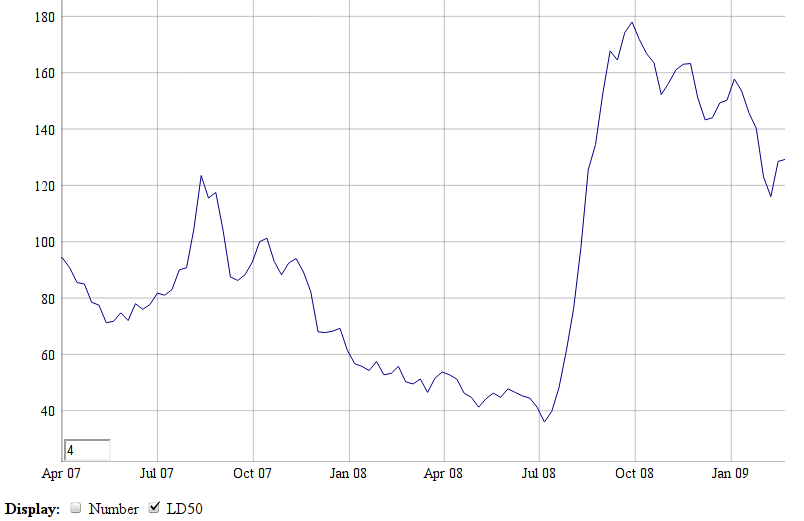
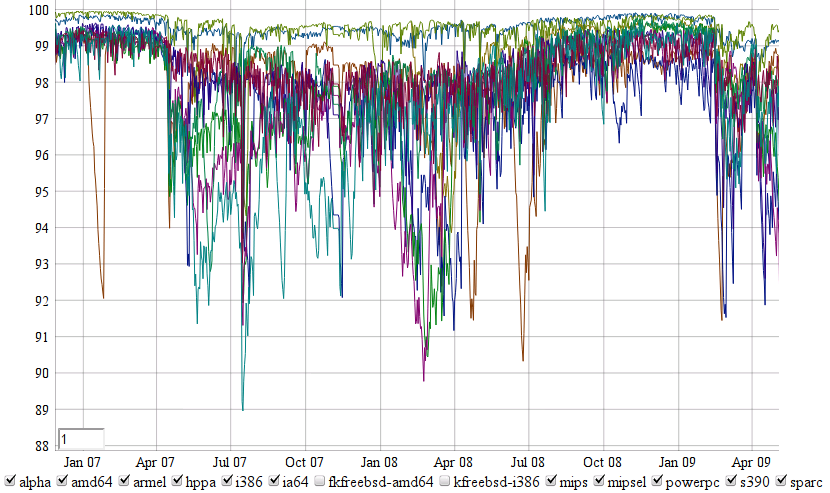
Owning the new now
Things are different now. That’s certain.
Or at least that’s what one of the marketing sites for my new employer has to say.
Back in March I started at Red Hat’s Brisbane office working in release engineering (or the “Release Configuration Management” team). Short summary: it’s been pretty fun so far.
Googling just now for something to link that provides some sort of context, I came upon a video with my boss (John Flanagan) and one of my colleagues (Jesse Keating) — neither of whom I’ve actually met yet — giving a talk to the ACM chapter at Northeastern University in Boston. (It’s an hour long, and doesn’t expect much background knowledge of Linux; but doesn’t go into anything in any great depth either)
My aim in deciding to go job hunting late last year was to get a large change of scenery and get to work with people who understood what I was doing — it eventually gets a bit old being a black box where computer problems go in, solutions come out, and you can only explain what happens in between with loose analogies before seeing eyes glaze over. Corporate environment, Fedora laptop, enterprise customers, and a zillion internal tools that are at least new to me, certainly counts as a pretty neat change of scenery; and I think I’ve now got about five layers of technical people between me and anyone who doesn’t have enough technical background to understand what I do on the customer side. Also, money appears in my bank account every couple of weeks, without having to send anyone a bill! It’s like magic!
The hiring process was a bit odd — mostly, I gather, because while I applied for an advertised position, the one I ended up getting was something that had been wanted for a while, but hadn’t actually had a request open. So I did a bunch of interviews for the job I was applying for, then got redirected to the other position, and did a few interviews for that without either me or the interviewers having a terribly clear idea what the position would involve. (I guess it didn’t really help that my first interview, which was to be with my boss’s boss, got rearranged because he couldn’t make it in due to water over the roads, and then Brisbane flooded; that the whole point of the position is that they didn’t have anyone working in that role closer than the Czech Republic is probably also a factor…)
As it’s turned out, that’s been a pretty accurate reflection of the role: I’ve mostly been setting my own priorities, which mostly means balancing between teaching myself how things work, helping out the rest of my team, and working with the bits of Red Hat that are local, or at least operate in compatible timezones. Happily, that seems to be working out fairly okay. (And at least the way I’ve been doing it isn’t much different to doing open source in general: “gah, this program is doing something odd. okay, find the source, see what it’s doing and why, and either (a) do something different to get what you want, or (b) fix the code. oh, and also, you now understand that program”)
As it turned out, that leads into the main culture shock I had on arriving: what most surprised me was actually the lack of differences compared to being involved in Debian — which admittedly might have been helped by a certain article hitting LWN just in time for my first day. “Ah, so that list is the equivalent of debian-devel. Good to know.” There’s a decent number of names that pop up that are familiar from Debian too, which is nice. Other comfortingly familiar first day activities were subscribing to more specific mailing lists, joining various IRC channels, getting my accounts setup and setting up my laptop. (Fedora was suggested, “not Debian” was recommended ;)
Not that everything’s the same — there’s rpm/yum versus dpkg/apt obviously, and there’s a whole morass of things to worry about working for a public company. But a lot of it fits into either “different to Debian, but not very” and “well, duh, Red Hat’s a for-profit, you have to do something like this, and that’s not a bad way of doing it”.
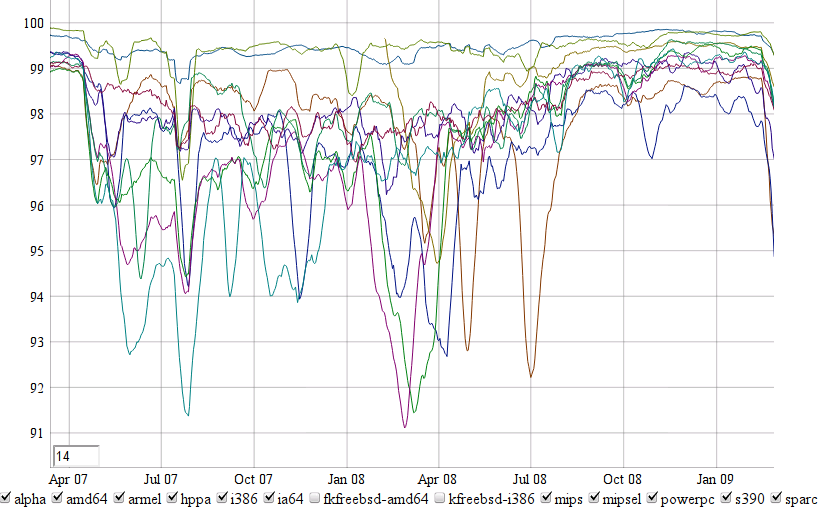
Hmm, not sure what else I can really talk about without at least running it by someone else to make sure it’s okay to talk about in public. I think there’s only a couple of things I’ve done so far that have gone via Fedora and are thus easy — the first was a quick python script to make publishing fedora torrents easier, and the other was a quick patch to the fedora buildsystem software to help support analytics. Not especially thrilling, though. I think Dennis is planning on throwing me into more Fedora stuff fairly soon, so hopefully that might change.